La velocidad máxima de una bomba de pistón es un factor crucial a tener en cuenta para asegurar un rendimiento óptimo y seguro en diferentes procesos industriales. Pero, ¿cómo se calcula esta velocidad? En este artículo, descubriremos los principios fundamentales y las variables que influyen en el cálculo de la velocidad máxima de una bomba de pistón. Tanto si eres un ingeniero en busca de conocimientos técnicos, como si simplemente estás interesado en el funcionamiento de estas poderosas máquinas, ¡este artículo está hecho para ti!
Las máquinas hidráulicas que convierten la energía hidráulica en energía mecánica se denominan turbinas, mientras que las máquinas hidráulicas que convierten la energía mecánica en energía hidráulica se denominan bombas. La energía hidráulica se presenta en forma de energía de presión. Si la energía mecánica se convierte en energía de presión debido a la fuerza centrífuga que actúa sobre el fluido, se denomina bomba centrífuga. Cuando la energía mecánica se convierte en energía hidráulica (o energía de presión) al succionar el fluido en un cilindro en el que un pistón oscila (cambia) que aplica el empuje al fluido y su energía hidráulica (energía de presión) aumenta. La bomba se llama bomba de pistón. En este artículo, comprendamos cómo podemos calcular la velocidad máxima de una bomba de pistón usando un problema de ejemplo.

Bomba de pistón
El siguiente diagrama muestra todas las partes principales de una bomba de pistón.
- Cilindro con pistón, vástago, biela y manivela.
- Tubo de aspiración
- tubo de entrega
- Válvula de aspiración
- Válvula de entrega

El diagrama esquemático anterior muestra una bomba de pistón de simple efecto que consta de un pistón que se mueve hacia adelante y hacia atrás en un cilindro muy ajustado. El movimiento del pistón se logra conectando el vástago del pistón a la manivela mediante una biela. La manivela es girada por un motor eléctrico.
Velocidad máxima de una bomba de pistón.
La velocidad máxima de una bomba de pistón está determinada por el hecho de que la presión en el cilindro durante la carrera de succión y entrega no debe caer por debajo de la presión de vapor del líquido que fluye a través de la tubería de succión y entrega. Si la presión en el cilindro es inferior a la presión de vapor, los gases disueltos se liberan del líquido y se produce cavitación. Además, no hay un flujo de fluido continuo, lo que significa que se produce una separación de fluidos.
La presión a la que se produce la separación se denomina presión de separación, y la altura de presión correspondiente a la presión de separación se denomina altura de presión de separación. Se denota por hSep.
Para el agua, el valor límite de la altura de presión de separación es (hSep) está 7,8 por debajo de la presión atmosférica o 10,3 – 7,8 = 2,5 m abs. La separación puede ocurrir durante la carrera de succión o durante la carrera de entrega. La velocidad máxima de la bomba de pistón durante la carrera de succión y entrega se calcula como:
(a) Velocidad máxima durante la carrera de succión
En el diagrama indicador dibujado a continuación, se puede ver que la carga de presión absoluta durante la carrera de succión es mínima al comienzo de la carrera.

Por favor habilite JavaScript
Esto significa que la separación sólo puede ocurrir al comienzo del derrame cerebral. En este caso los músculos abdominales. El nivel de presión en el cilindro al inicio de la carrera corresponde al nivel de presión de separación (h).Sep).
hSep =HCajero automático -hS-hcomo
hcomo =HCajero automático -hS-hSep
En general, los valores de hSep yhS (altura de succión) están dadas y por lo tanto hcomo Se puede determinar el nivel de presión debido a la aceleración al inicio de la carrera de succión. El valor de h.como también está dado por
Ecuación como sigue

La ecuación de los dos valores de surgió de las dos ecuaciones anteriores.

….. Ecuación(a)
A partir de la ecuación (a) anterior, se puede determinar el valor de ω y, por tanto, la velocidad N. Esta velocidad es la velocidad máxima de la bomba de pistón sin separación durante la carrera de succión.
(b) Velocidad máxima durante la carrera de entrega
Durante la carrera de entrega, la probabilidad de separación sólo ocurre al final de la carrera de entrega. El nivel de presión en el cilindro está al final de la carrera de entrega.
= (HCajero automático +hD) -HAnuncio metro (abs.)
Para evitar la separación, la altura de presión anterior debe ser mayor que la presión de separación.
cabeza (hSep). En casos límite
hSep = (HCajero automático +hD) -HAnuncio
o
hAnuncio = (HCajero automático +hD) -HSep
Pero hAnuncio La altura de presión debida a la aceleración al final de la carrera de entrega también está dada por
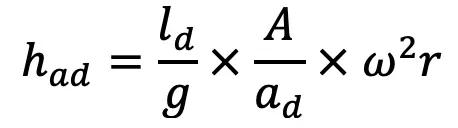
Igualando los dos valores de hAnuncio obtenemos
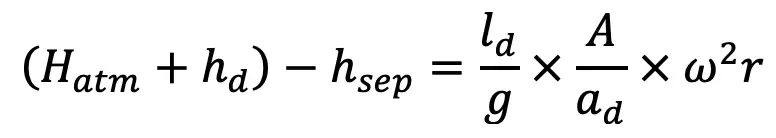
….. Ecuación(b)
A partir de la ecuación (b) anterior, se puede calcular el valor de ω y, por tanto, las velocidades N. Esta es la velocidad máxima de la bomba de pistón sin desconexión solo durante la carrera de impulsión.
El mínimo de las dos velocidades dadas en los dos casos anteriores (a) y (b) es la velocidad máxima de la bomba de pistón sin separación durante las carreras de succión y entrega.
Resolvamos un problema de ejemplo para calcular la velocidad máxima de una bomba de pistón.
Calcular la velocidad máxima de una bomba de pistón
Planteamiento del problema: Determine la velocidad máxima de una bomba de pistón de simple efecto para evitar la separación que ocurre a 3,0 m de profundidad de agua (abs.). La bomba tiene un cilindro con un diámetro de 10 cm y una longitud de carrera de 20 cm. La bomba aspira agua de un sumidero y la bombea a un tanque. El nivel del agua en el sumidero está a 3,5 m por debajo del eje de la bomba y en el tanque el nivel del agua está a 13 m por encima del eje de la bomba. El diámetro y la longitud de la tubería de succión son de 4 cm y 5 m, respectivamente, mientras que el diámetro y la longitud de la tubería de impulsión son de 3 cm y 20 m, respectivamente. Tomemos una altura de presión atmosférica = 10,3 m de columna de agua.
Respuesta:
datos dados
Altura de presión de separación, hSep = 3,0 m de columna de agua (abs.)
Diámetro del cilindro, D = 10 cm = 0,10 m
Longitud de carrera L = 20 cm = 0,20 m
Radio del cigüeñal, r = L /2 = 0,2/2 = 0,10 m
Cabezal de succión, hS = 3,5 metros
cabeza, hD = 13m
Diámetro del tubo de aspiración, es decirS = 4 cm = 0,04 m
Longitud del tubo de aspiración, lS = 5 metros
Diámetro de la línea de entrega, es decirD = 3 cm = 0,03 m
Longitud de la línea de entrega, lD = 20 metros
Altitud de presión atmosférica, HCajero automático= 10,3 metros
(I) Velocidad máxima de la bomba de pistón. durante la carrera de succión sin separación viene dada por la relación dada por la ecuación (a).
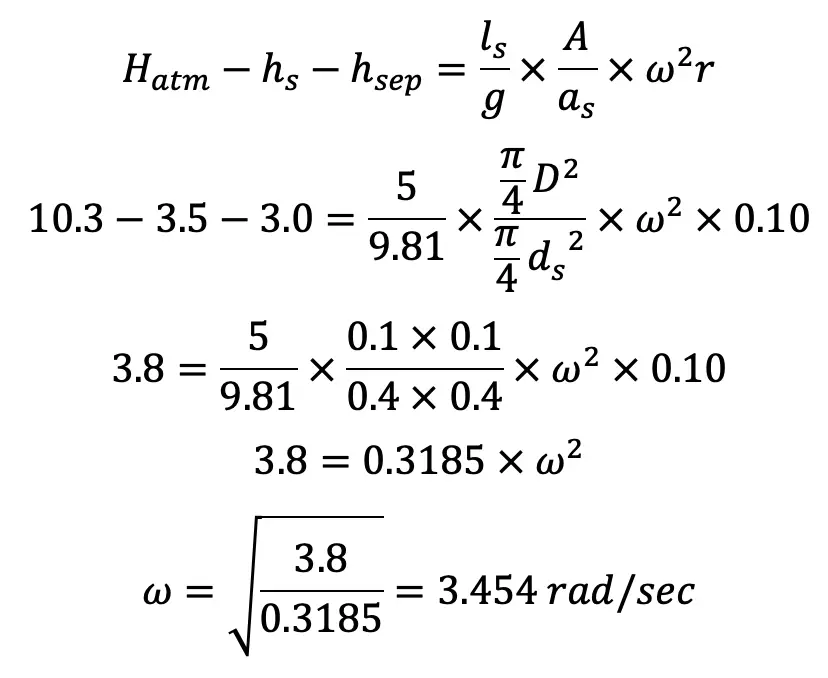
La velocidad angular de una bomba de pistón es 3,454 rad/s. A partir de la velocidad angular podemos calcular la velocidad de la siguiente manera.
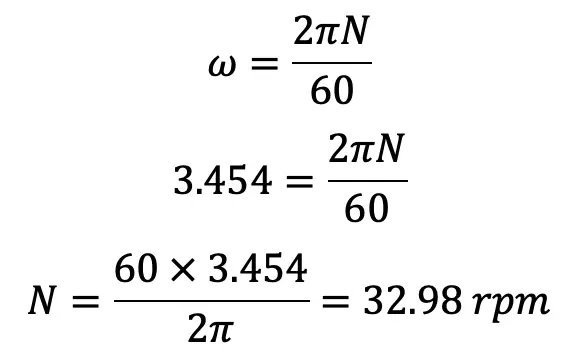
La velocidad máxima de una bomba de pistón durante la carrera de succión sin desconexión es de 32,98 rpm.
(ii) Velocidad máxima de la bomba de pistón. durante la carrera de entrega sin separación resulta de la ecuación (b),
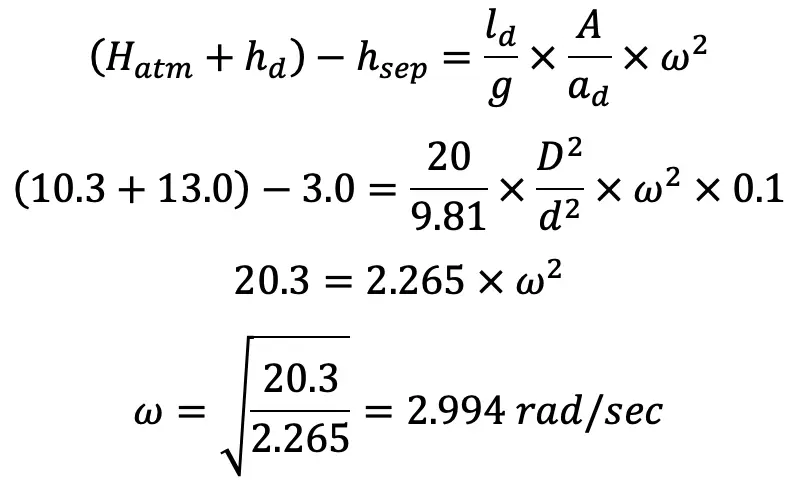
La velocidad angular de una bomba de pistón es 2,994 rad/s. A partir de la velocidad angular podemos calcular la rapidez de la siguiente manera.
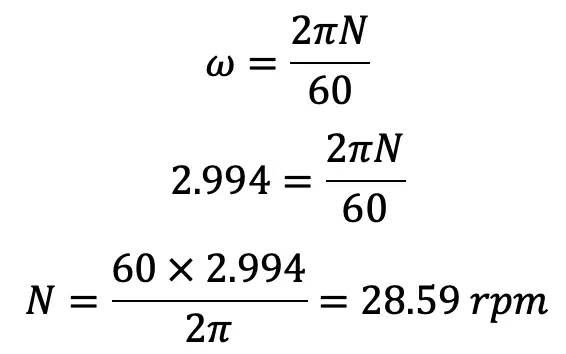
La velocidad máxima de la bomba de pistón durante la carrera de impulsión sin desconexión es de 28,59 rpm.
La mínima de las dos velocidades dadas por las ecuaciones anteriores es la velocidad máxima de la bomba sin separación.
La velocidad máxima de la bomba de pistón sin separación para el problema dado es 28,59 rpm.
De esta manera podemos calcular la velocidad máxima de una bomba de pistón a partir de las entradas dadas. Háganos saber lo que piensa sobre este artículo en la sección de comentarios a continuación.
[automatic_youtube_gallery type=»search» search=»¿Cómo se calcula la velocidad máxima de una bomba de pistón?
» limit=»1″]
La Bomba de Émbolo
Las máquinas hidráulicas que convierten la energía hidráulica en energía mecánica se llaman turbinas, mientras que las máquinas hidráulicas que convierten la energía mecánica en energía hidráulica se llaman bombas. La energía hidráulica se encuentra en forma de energía de presión. Si la energía mecánica se convierte en energía de presión mediante la fuerza centrífuga que actúa sobre el fluido, la máquina hidráulica se llama bomba centrífuga. Si la energía mecánica se convierte en energía hidráulica (o energía de presión) al succionar el líquido en un cilindro en el que un émbolo se mueve alternativamente hacia atrás y hacia adelante, lo cual ejerce una fuerza sobre el líquido y aumenta su energía hidráulica (energía de presión), la bomba se conoce como bomba de émbolo. En este artículo, vamos a entender cómo calcular la velocidad máxima de una bomba de émbolo con un problema de ejemplo.
Bomba de Émbolo
El siguiente esquema representa todas las partes principales de una bomba de émbolo:
- Cilindro con un émbolo, varilla de émbolo, biela y cigüeñal.
- Tubería de succión.
- Tubería de entrega.
- Válvula de succión.
- Válvula de entrega.
El esquema anterior muestra una bomba de émbolo de simple efecto, que consiste en un émbolo que se mueve hacia adelante y hacia atrás en un cilindro de ajuste preciso. El movimiento del émbolo se obtiene mediante la conexión de la varilla del émbolo al cigüeñal mediante una biela. El cigüeñal se gira mediante un motor eléctrico.
Velocidad Máxima de una Bomba de Émbolo
La velocidad máxima de una bomba de émbolo se determina por el hecho de que la presión en el cilindro durante el tiempo de succión y el tiempo de entrega no debe caer por debajo de la presión de vapor del líquido que fluye a través de las tuberías de succión y entrega. Si la presión en el cilindro es inferior a la presión de vapor, los gases disueltos se liberarán del líquido y se producirá una cavitación. Además, no existirá un flujo continuo de líquido, lo que significa que se producirá una separación del líquido.
La presión en la cual ocurre la separación se conoce como presión de separación y la altura correspondiente a la presión de separación se conoce como altura de presión de separación, que se denota como hsep.
Para el agua, el valor límite de la altura de presión de separación (hsep) es de 7.8 por debajo de la altura de presión atmosférica o 10.3 – 7.8 = 2.5 m abs. La separación puede ocurrir durante el tiempo de succión o durante el tiempo de entrega. La velocidad máxima de la bomba de émbolo durante los tiempos de succión y entrega se calcula de la siguiente manera:
(a) Velocidad Máxima durante el Tiempo de Succión
A partir del diagrama del indicador, dibujado en el siguiente, es evidente que la altura de presión absoluta durante el tiempo de succión es mínima al comienzo del tiempo.
El efecto combinado de la aceleración y la fricción en las tuberías de succión y entrega en el diagrama del indicador.
Así, la separación solo puede ocurrir al comienzo del tiempo. En ese caso, la altura de presión absoluta en el cilindro al comienzo del tiempo será igual a la altura de presión de separación (hsep).
hsep = Hatm – hs – hashas = Hatm – hs – hsep
Generalmente, se dan los valores de hsep y hs (altura de succión) y, por lo tanto, has, la altura de presión debido a la aceleración al comienzo del tiempo de succión, se puede obtener. El valor de has también se da por la siguiente ecuación:
has = (2 × V) / (g × A) – hs
Igualando los dos valores de has dados por las dos ecuaciones anteriores:
has = (2 × V) / (g × A) – hs = Hatm – hs – hsep
De la ecuación anterior, se puede obtener el valor de ω y, por lo tanto, la velocidad N. Esta velocidad es la velocidad máxima de la bomba de émbolo sin separación durante el tiempo de succión.
(b) Velocidad Máxima durante el Tiempo de Entrega
Durante el tiempo de entrega, la probabilidad de separación es solo al final del tiempo. La altura de presión en el cilindro al final del tiempo de entrega será
(Hatm + hd) – had m (abs.)
Si se debe evitar la separación, la altura de presión anterior debe ser mayor que la altura de presión de separación (hsep). En el caso límite:
had = (Hatm + hd) – hsep
Pero had, la altura de presión debido a la aceleración al final del tiempo de entrega, también se da por:
had = (2 × V) / (g × A) + hd
Igualando los dos valores de had:
(2 × V) / (g × A) + hd = (Hatm + hd) – hsep
De la ecuación anterior, se puede calcular el valor de ω y, por lo tanto, las velocidades N. Esta es la velocidad máxima de la bomba de émbolo sin separación durante el tiempo de entrega solamente.
La velocidad mínima de las dos velocidades dadas por los dos casos anteriores (a) y (b) es la velocidad máxima de la bomba de émbolo sin separación durante los tiempos de succión y entrega.
Resolviendo un Problema de Ejemplo para Calcular la Velocidad Máxima de una Bomba de Émbolo
Problema: Encuentra la velocidad máxima de una bomba de émbolo de simple efecto para evitar la separación, que ocurre a 3.0 m de agua (abs.). La bomba tiene un cilindro de diámetro de 10 cm y una longitud de carrera de 20 cm. La bomba extrae agua de un sumidero y la entrega a un tanque. El nivel de agua en el sumidero está a 3.5 m por debajo del eje de la bomba y en el tanque, el nivel de agua está a 13 m por encima del eje de la bomba. El diámetro y la longitud de la tubería de succión son de 4 cm y 5 m, mientras que el diámetro y la longitud de la tubería de entrega son de 3 cm y 20 m, respectivamente. Tome la altura de presión atmosférica como 10.3 m de agua.
Respuesta:
Datos dados:
- Altura de presión de separación, hsep = 3.0 m de agua (abs.)
- Diámetro del cilindro, D = 10 cm = 0.10 m
- Longitud de carrera L = 20 cm = 0.20 m
- Radio del cigüeñal, r = L / 2 = 0.2 / 2 = 0.10 m
- Altura de succión, hs = 3.5 m
- Altura de entrega, hd = 13 m
- Diámetro de la tubería de succión, ds = 4 cm = 0.04 m
- Longitud de la tubería de succión, ls = 5 m
- Diámetro de la tubería de entrega, dd = 3 cm = 0.03 m
- Longitud de la tubería de entrega, ld = 20 m
- Altura de presión atmosférica, Hatm = 10.3 m
(i) La velocidad máxima de la bomba de émbolo durante el tiempo de succión sin separación se obtiene de la relación dada por la ecuación (a)
La velocidad angular de una bomba de émbolo es de 3.454 rad/seg. A partir de la velocidad angular, podemos calcular la velocidad de la siguiente manera:
La velocidad máxima de la bomba de émbolo durante el tiempo de succión sin separación es de 32.98 RPM.
(ii) La velocidad máxima de la bomba de émbolo durante el tiempo de entrega sin separación se obtiene de la ecuación (b)
La velocidad angular de una bomba de émbolo es de 2.994 rad/seg. A partir de la velocidad angular, podemos calcular la velocidad de la siguiente manera:
La velocidad máxima de la bomba de émbolo durante el tiempo de entrega sin separación es de 28.59 RPM.
El mínimo de las dos velocidades dadas por las ecuaciones anteriores es la velocidad máxima de la bomba sin separación.
La velocidad máxima de la bomba de émbolo sin separación para el problema dado es de 28.59 RPM.
Así es como podemos calcular la velocidad máxima de una bomba de émbolo a partir de los datos proporcionados. Háganos saber qué opina sobre este artículo en la sección de comentarios a continuación.
