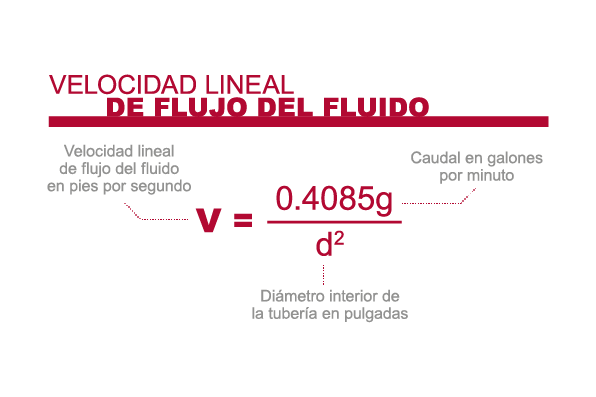
Cuando hablamos de fluidos, es común referirse a diferentes aspectos que los caracterizan, como su flujo, velocidad y descarga. Estos elementos son fundamentales para comprender cómo se comportan los fluidos en distintas situaciones y qué impacto tienen en diversos procesos industriales. En este artículo, exploraremos los diferentes tipos de flujo de fluido, así como la importancia de la velocidad de fluido y cómo afecta a la descarga. Desde la fluidez laminar hasta la turbulencia, descubriremos cómo estos conceptos influyen en nuestra vida diaria y en el mundo que nos rodea. Prepárate para sumergirte en el fascinante mundo de los fluidos y descubre qué hay más allá de su apariencia líquida.
En mecánica de fluidos, existen diferentes tipos de flujos de fluidos y un estudio de estos tipos de flujos de fluidos nos ayudará a determinar la descarga del flujo, la velocidad y la aceleración de los fluidos. Una vez conocida la velocidad, se pueden determinar fácilmente la distribución de presión y las fuerzas que actúan sobre el fluido. Analicemos en detalle estos tipos de flujos de fluidos.


Tipos de flujos de fluidos
A continuación se muestran los diferentes tipos de flujo de fluido que podemos utilizar para determinar la velocidad y aceleración del fluido.
- Flujos constantes e inestables
- Flujos uniformes y desiguales
- Flujos laminares y turbulentos.
- Flujos compresibles e incompresibles.
- Flujos rotativos y rotacionales.
- Flujos unidimensionales, bidimensionales y tridimensionales.
1. Flujos estacionarios e inestables
El flujo estacionario es el tipo de flujo en el que las propiedades del fluido como velocidad, presión, densidad, etc. en un punto no cambian con el tiempo.
Entonces, para un flujo constante podemos escribir matemáticamente
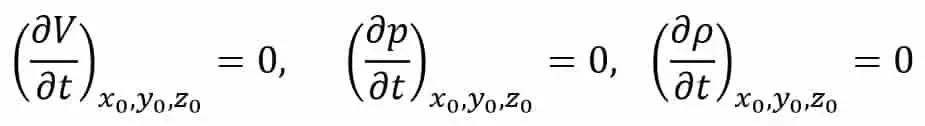
donde (x0Sí0p.ej0) es un punto fijo en un campo fluido.
El flujo inestable es el tipo de flujo en el que la velocidad, presión o densidad en un punto cambia con el tiempo.
Por tanto, podemos escribir matemáticamente para flujos inestables.
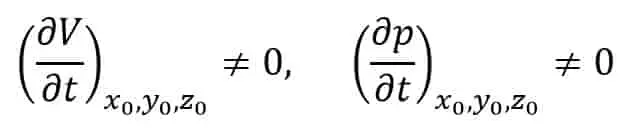
2. Flujos uniformes y desiguales
Por favor habilite JavaScript
Un flujo uniforme se define como el tipo de flujo en el que la velocidad en un momento dado no cambia con respecto al espacio (es decir, la longitud de la dirección del flujo).
Matemáticamente hablando, podemos escribir para un flujo fluido.
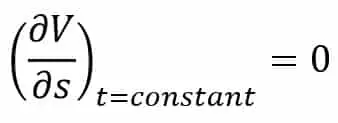
Dónde
∂V = cambio de velocidad
∂s = longitud del flujo en dirección S
El flujo no uniforme es el tipo de flujo en el que la velocidad cambia con respecto al espacio en un momento dado.
Por tanto, podemos escribir matemáticamente para la no uniformidad.

3. Flujos laminares y turbulentos
El flujo laminar se define como el tipo de flujo en el que las partículas de fluido se mueven a lo largo de trayectorias o líneas de corriente bien definidas y todas las líneas de corriente son rectas y paralelas.
Así, las partículas se mueven en capas o capas y se deslizan suavemente sobre la capa adyacente. Este tipo de flujo también se denomina flujo aerodinámico o flujo viscoso.
El flujo turbulento es el tipo de flujo en el que las partículas de fluido se mueven en zigzag. El movimiento en zigzag de las partículas del líquido provoca la formación de vórtices, lo que es responsable de una gran pérdida de energía.
En un flujo de tubería, el tipo de flujo está determinado por un número adimensional VD/v se llama número de Reynolds.
Número de Reynolds = VD/v
Dónde
D = diámetro de la tubería
V = Velocidad promedio del flujo en la tubería
v = Viscosidad cinemática del líquido
Si el número de Reynolds es menor que 2000, se llama flujo laminar.
Si el número de Reynolds es superior a 4000, el flujo se denomina turbulento.
Si el número de Reynolds está entre 2000 y 4000, el flujo puede ser laminar o turbulento.
4. Flujos compresibles e incompresibles
El flujo compresible es un flujo en el que la densidad del fluido cambia de un punto a otro.
En otras palabras, el flujo compresible se puede definir como una densidad no constante (ρ) del fluido.
Matemáticamente hablando para flujo compresible
ρ ≠ constante
Los flujos incompresibles son flujos en los que la densidad del flujo de fluido es constante. Los líquidos generalmente son incompresibles mientras que los gases son comprimibles.
Matemáticamente hablando, para flujo incompresible
ρ = constante
5. Flujos rotacionales y no rotacionales
El flujo rotacional es el tipo de flujo en el que las partículas de fluido, mientras fluyen a lo largo de líneas de corriente, también giran alrededor de su propio eje. Y cuando las partículas de fluido no giran alrededor de su propio eje cuando fluyen a lo largo de líneas de corriente, este tipo de flujo se llama flujo rotacional.
6. Flujos unidimensionales, bidimensionales y tridimensionales
Flujo unidimensional es el flujo en el que el parámetro de flujo, al igual que la velocidad, es función del tiempo y solo una coordenada espacial, digamos x.
En un flujo unidimensional constante, la velocidad es sólo función de una coordenada espacial. Se supone que la variación de las velocidades en las otras dos direcciones mutuamente perpendiculares es insignificante.
Por tanto, matemáticamente para un flujo unidimensional:
u = f(x), v = 0 y w = 0
Aquí u, v y w son componentes de la velocidad en las direcciones x, y y z, respectivamente.
Flujo bidimensional es el tipo de flujo que es función del tiempo y de dos coordenadas espaciales rectangulares, por ejemplo x e y.
En un flujo bidimensional estacionario, la velocidad es sólo función de dos coordenadas espaciales. La variación o velocidad en la tercera dirección es insignificante.
Entonces matemáticamente para el flujo bidimensional
tu = f1(x, y), v = f2(x, y) y w = 0
El flujo tridimensional es de este tipo. Flujo en el que la velocidad es función del tiempo y de tres direcciones mutuamente perpendiculares.
Pero para un flujo tridimensional estable, los parámetros del fluido son sólo funciones de tres coordenadas espaciales (x, y, z).
Entonces, matemáticamente hablando, para un flujo tridimensional
tu = f1(x, y, z), v = f2(x, y, z) y w = f3(x, y, z)
Estos son 6 tipos diferentes de flujo de fluido que nos ayudarán a determinar la velocidad y aceleración del flujo de fluido en los próximos artículos.
Ahora conocemos los tipos de flujo, pero ¿cómo podemos calcular la cantidad de flujo que drena por la tubería si ya conocemos la velocidad?
Caudal (Q)
Se define como la cantidad de fluido que fluye a través de un tramo de tubería o conducto por segundo. Para un fluido (o fluido) incompresible, el flujo o tasa de descarga se expresa como el volumen de fluido que fluye a través de la sección por segundo.
Para fluidos compresibles, la velocidad del flujo generalmente se expresa como el peso del fluido que fluye a través de la sección.
- Para líquidos, las unidades de Q son m3/s o litros/s
- Para gases, las unidades de Q son kgf/s o Newton/s
Imagine un líquido que fluye a través de una tubería y luego se drena a través de la tubería.
Q = A×V
Dónde
A = área de la sección transversal de la tubería
V = Velocidad promedio del fluido sobre la sección
Ecuación de continuidad
A partir de la *ley de conservación de la masa podemos escribir la ecuación de continuidad.
*Ley de Conservación de la masa: La ley de conservación de la masa establece que la masa no se puede crear ni destruir, sino que se transforma de una forma a otra.
Como ya se mencionó, la ecuación basada en la ley de conservación de la masa se llama ecuación de continuidad. Para un líquido que fluye a través de todas las secciones transversales de una tubería, la cantidad de líquido por segundo es constante.
Considere dos secciones transversales de una tubería, como se muestra en la siguiente figura.

Dejar
v1 = velocidad media en la sección transversal 1-1
ρ1 = densidad en la sección 1-1
A1 = área de tubería en la sección 1-1
y V2ρ2 A2son los valores correspondientes en la Sección 2-2.
El caudal en la sección 1-1 = ρ1 A1v1
El caudal en la sección 2-2 = ρ2 A2v2
Según la ley de conservación de la masa mencionada anteriormente.
Caudal en la sección 1-1 = caudal en la sección 2-2
La ecuación anterior se aplica tanto a fluidos compresibles como incompresibles y se llama ecuación de continuidad.
Si el fluido es incompresible entonces ρ1 = ρ2y la ecuación de continuidad anterior se reduce de la siguiente manera
A1v1 = Un2v2
Leer más sobre la ecuación de continuidad en tres dimensiones y también en coordenadas polares
Resolvamos un problema de ejemplo para encontrar fugas de fluido a través de una tubería usando la ecuación de continuidad anterior.
Planteamiento del problema: Los diámetros de tubería de los tramos 1 y 2 son 10 cm y 15 cm, respectivamente. Encuentre la descarga a través de la tubería si la velocidad del agua que fluye a través de la tubería en la sección 1 es de 5 m/s. Determine también la velocidad en la sección 2.
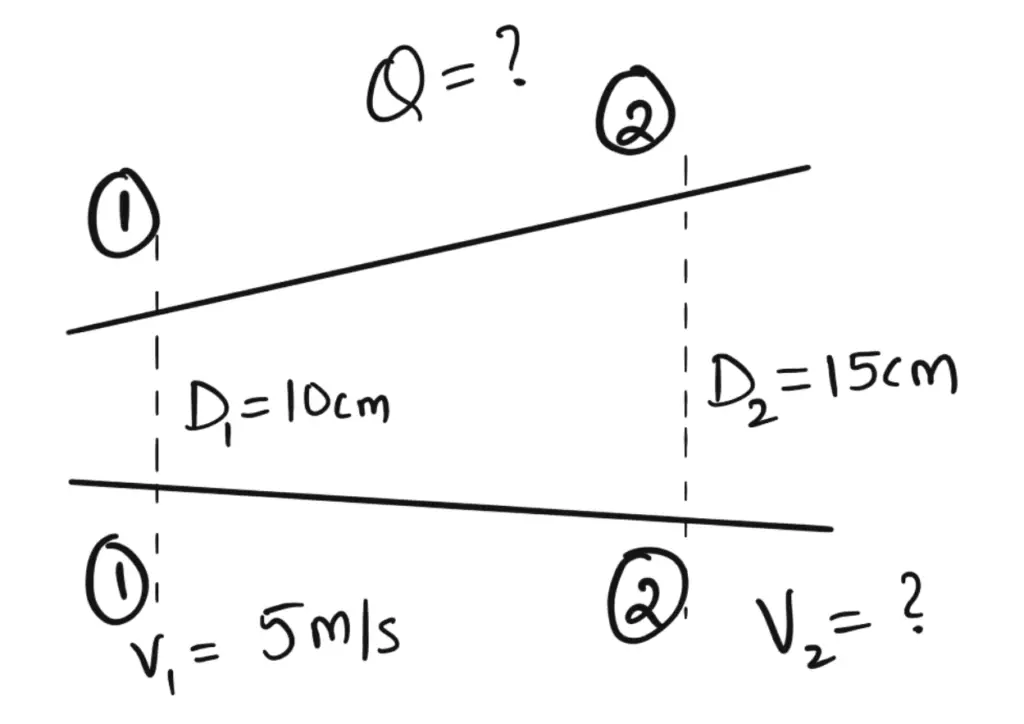
Solución:
Dado que
Sección 1 Diámetro de tubería D1 = 10 cm = 0,1 m
Área de sección transversal A1 = (ℼ/4) (D1)2 = 0,007854 m2
Velocidad del flujo en la sección 1 V1 = 5 m/s
Sección 2 Diámetro de tubería D2 = 15 cm = 0,15 m
Área de sección transversal A2 = (ℼ/4) (D1)2 = 0,01767 m2
Alivio (Q) Pensé que era el silbato.
q = a1 ×V1
Q = 0,007854 × 5
Q = 0,03927 m3/S
Velocidad en el tramo 2 (v2)
Sabemos por la ecuación de continuidad anterior
A1v1 = Un2v2
0,007854 × 5 = 0,01767 × V2
v2 = 2,22 m/s
Esto le permite calcular la descarga o velocidad de cualquier fluido dadas las entradas suficientes presentadas anteriormente.
¿Puedes resolver un problema de ejemplo sobre este tema?
Problema de práctica: Una tubería de 30 cm de diámetro que transporta agua se ramifica en tuberías IWO de 20 cm y 15 cm de diámetro, respectivamente. Si la velocidad promedio en la tubería de 30 cm de diámetro es 2.5 m/s, encuentre la descarga en esta tubería. Además, determine la velocidad en una tubería de 15 cm de diámetro si la velocidad promedio en una tubería de 20 cm de diámetro es 2 m/s.
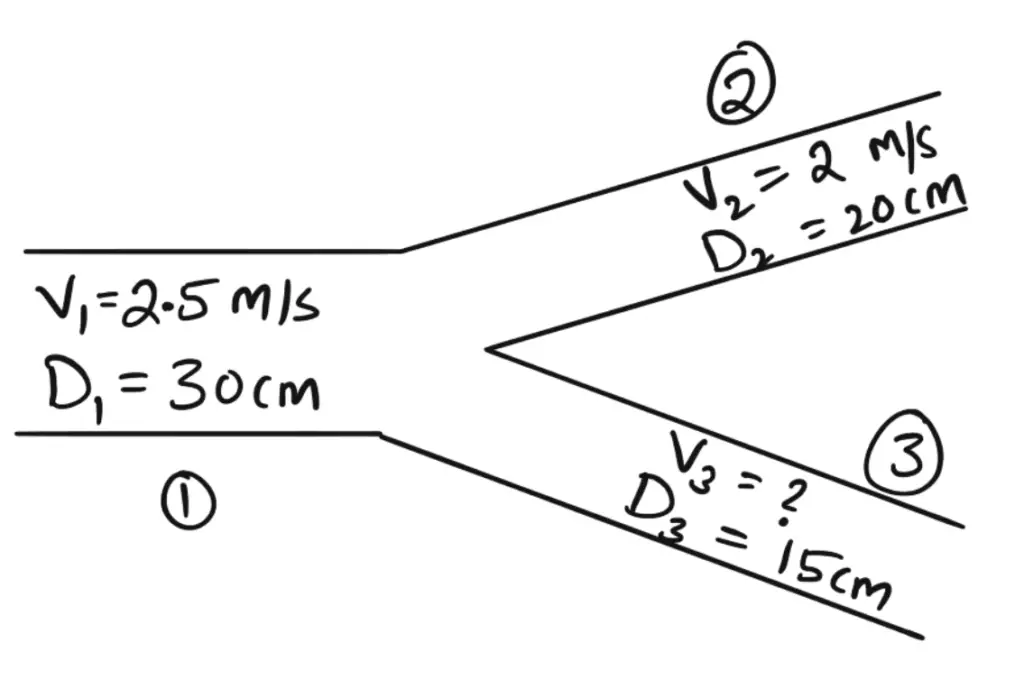
Resuélvelo y comparte la respuesta con nosotros en la sección de comentarios a continuación. Te ayudare.
Hemos discutido los temas básicos de la mecánica de fluidos de la siguiente manera.
- Las propiedades físicas de los líquidos (densidad, viscosidad y tensión superficial).
- ley de pascal
- Ley hidrostática y principio de Arquímedes.
- Medir la presión con monómetros.
- Calcular el peso levantado por el gato hidráulico.
- Calcular la presión atmosférica utilizando las leyes isotérmica y adiabática.
[automatic_youtube_gallery type=»search» search=»Diferentes tipos de flujo de fluido, velocidad de fluido y descarga.
» limit=»1″]
En Mecánica de Fluidos, existen diferentes tipos de flujo de fluidos, y el estudio de estos tipos de flujo nos ayudará a determinar el caudal, la velocidad y la aceleración del fluido. Una vez que se conoce la velocidad, podemos determinar sin esfuerzo la distribución de presión y las fuerzas que actúan sobre el fluido. Veamos en detalle estos tipos de flujos de fluidos.
Tipos de flujos de fluidos
A continuación se presentan los diferentes tipos de flujos de fluidos que nos ayudan a determinar la velocidad y la aceleración del fluido.
1. Flujos estables e inestables
El flujo estable se define como ese tipo de flujo en el que las características del fluido, como la velocidad, la presión, la densidad, etc., en un punto, no cambian con el tiempo.
Así que para un flujo estable, matemáticamente podemos escribir:
Velocidad (V) = constante
Donde (x0, y0, z0) es un punto fijo en un campo de fluido.
El flujo inestable es ese tipo de flujo en el que la velocidad, la presión o la densidad en un punto cambian con respecto al tiempo.
Entonces, matemáticamente, para un flujo inestable, podemos escribir:
Velocidad (V) = función del tiempo
2. Flujos uniformes y no uniformes
El flujo uniforme se define como ese tipo de flujo en el que la velocidad en un momento dado no cambia con respecto al espacio (es decir, la longitud de la dirección del flujo).
Matemáticamente, para un flujo uniforme, podemos escribir:
ΔV = Cambio de velocidad
Δs = Longitud del flujo en la dirección S
El flujo no uniforme es ese tipo de flujo en el que la velocidad en un momento dado cambia con respecto al espacio.
Entonces, matemáticamente para un flujo no uniforme, podemos escribir:
ΔV ≠ Cambio de velocidad
3. Flujos laminar y turbulento
El flujo laminar se define como ese tipo de flujo en el que las partículas del fluido se mueven a lo largo de trayectorias bien definidas o líneas de corriente y todas las líneas de corriente son rectas y paralelas.
El flujo turbulento es ese tipo de flujo en el que las partículas del fluido se mueven de manera zigzagueante. Debido al movimiento de las partículas del fluido de manera zigzagueante, se producen vórtices que son responsables de una alta pérdida de energía.
Para un flujo en una tubería, el tipo de flujo se determina por un número adimensional llamado número de Reynolds (Re).
Si el número de Reynolds es menor que 2000, el flujo se llama laminar.
Si el número de Reynolds es mayor que 4000, se llama flujo turbulento.
Si el número de Reynolds está entre 2000 y 4000, el flujo puede ser laminar o turbulento.
4. Flujos compresibles e incompresibles
El flujo compresible es ese tipo de flujo en el que la densidad del fluido cambia de punto a punto.
En otras palabras, el flujo compresible se puede definir como la densidad (ρ) no es constante para el fluido.
Entonces, matemáticamente, para un flujo compresible:
ρ ≠ Constante
El flujo incompresible es ese tipo de flujo en el que la densidad es constante para el flujo de fluido. Los líquidos son generalmente incompresibles, mientras que los gases son compresibles.
Matemáticamente, para un flujo incompresible:
ρ = Constante
5. Flujos rotacionales e irrotacionales
El flujo rotacional es ese tipo de flujo en el que las partículas del fluido, mientras fluyen a lo largo de las líneas de corriente, también giran alrededor de su propio eje. Y si las partículas del fluido, mientras fluyen a lo largo de las líneas de corriente, no giran alrededor de su propio eje, entonces se llama flujo irrotacional.
6. Flujos unidimensionales, bidimensionales y tridimensionales
El flujo unidimensional es aquel en el que el parámetro de flujo, como la velocidad, es una función del tiempo y de una sola coordenada espacial, digamos x.
El flujo bidimensional es ese tipo de flujo en el que el parámetro de flujo es una función del tiempo y de dos coordenadas espaciales rectangulares, digamos x e y.
El flujo tridimensional es ese tipo de flujo en el que la velocidad es una función del tiempo y de tres direcciones mutuamente perpendiculares, pero para un flujo estable tridimensional, los parámetros del fluido son funciones de tres coordenadas espaciales (x, y, z) solamente.
Estos son los 6 diferentes tipos de flujos de fluidos que nos ayudan a determinar la velocidad y la aceleración del flujo de fluido en los próximos artículos.
Ahora que conocemos los diferentes tipos de flujo, ¿cómo podemos calcular la cantidad de flujo a través de una tubería si ya conocemos la velocidad?
Tasa de flujo (Q)
Se define como la cantidad de fluido que fluye por segundo a través de una sección de una tubería o canal. Para un fluido incompresible (o líquido), la tasa de flujo o descarga se expresa como el volumen de fluido que fluye a través de la sección por segundo.
Para fluidos compresibles, la tasa de flujo se expresa generalmente como el peso de fluido que fluye a través de la sección.
Para líquidos, las unidades de Q son m3/s o litros/s.
Para gases, las unidades de Q son kgf/s o Newton/s.
Consideremos un líquido que fluye a través de una tubería, entonces la descarga a través de la tubería es:
Q = A × V
Donde
A = Área de la sección transversal de la tubería
V = Velocidad promedio del fluido a través de la sección
Ecuación de continuidad
A partir de la ley de conservación de la masa, podemos escribir la ecuación de continuidad.
Ley de conservación de la masa: La ley de conservación de la masa establece que la masa no puede ser creada ni destruida, sino que se transforma de una forma a otra.
Como hemos establecido la ecuación basada en la ley de conservación de la masa, se llama ecuación de continuidad. Para un fluido que fluye a través de una tubería en todas las secciones transversales, la cantidad de fluido por segundo es constante.
Consideremos dos secciones transversales de una tubería como se muestra en la siguiente figura:
Sea
V1 = Velocidad promedio en la sección 1-1
ρ1 = Densidad en la sección 1-1
A1 = Área de la tubería en la sección 1-1
Y V2, ρ2, A2, son los valores correspondientes en la sección 2-2.
La tasa de flujo en la sección 1-1 = ρ1 A1 V1
La tasa de flujo en la sección 2-2 = ρ2 A2 V2
De acuerdo con la ley de conservación de la masa, a partir de lo anterior,
Tasa de flujo en la sección 1-1 = Tasa de flujo en la sección 2-2
La ecuación anterior es aplicable tanto a los fluidos compresibles como a los incompresibles y se llama ecuación de continuidad.
Si el fluido es incompresible, entonces ρ1 = ρ2, y la ecuación de continuidad anterior se reduce de la siguiente manera:
A1 V1 = A2 V2
Lee más sobre la ecuación de continuidad en tres dimensiones y también en coordenadas polares.
Resolvamos un problema ejemplo para encontrar la descarga de fluido a través de una tubería con la ayuda de la ecuación de continuidad anterior.
Enunciado del problema: Los diámetros de la tubería en las secciones 1 y 2 son de 10 cm y 15 cm respectivamente. Encuentra la descarga a través de la tubería si la velocidad del agua que fluye a través de la tubería en la sección 1 es de 5 m/s. Determina también la velocidad en la sección 2.
Solución:
Dado que
Diámetro de la tubería en la sección 1 (D1) = 10 cm = 0.1 m
Área de la sección transversal (A1) = (π/4) (D1)2 = 0.007854 m2
Velocidad de flujo en la sección 1 (V1) = 5 m/s
Diámetro de la tubería en la sección 2 (D2) = 15 cm = 0.15 m
Área de la sección transversal (A2) = (π/4) (D2)2 = 0.01767 m2
La descarga (Q) a través de la tubería es:
Q = A1 × V1
Q = 0.007854 × 5
Q = 0.03927 m3/s
Velocidad en la sección 2 (V2)
Sabemos, a partir de la ecuación de continuidad anterior:
A1V1 = A2V2
0.007854 × 5 = 0.01767 × V2
V2 = 2.22 m/s
De esta manera, puedes calcular la descarga o velocidad de cualquier fluido si conoces las entradas suficientes como se ilustra arriba.
¿Puedes resolver un problema ejemplo sobre este mismo tema?
Problema de ejercicio: Una tubería de 30 cm de diámetro que transporta agua se bifurca en dos tuberías de diámetros de 20 cm y 15 cm respectivamente. Si la velocidad promedio en la tubería de 30 cm de diámetro es de 2.5 m/s, encuentre la descarga en esta tubería. Además, determine la velocidad en la tubería de 15 cm si la velocidad promedio en la tubería de 20 cm de diámetro es de 2 m/s.
Resuélvelo y déjanos la respuesta en la sección de comentarios a continuación. Te ayudaré.
Hemos estado discutiendo temas básicos de Mecánica de Fluidos como los siguientes:
– Propiedades físicas de los fluidos (densidad, viscosidad y tensión superficial)
– Ley de Pascal
– Ley hidrostática y principio de Arquímedes
– Medición de la presión con manómetros
– Cálculo del peso levantado por un gato hidráulico
– Cálculo de la presión atmosférica con las leyes isotérmica y adiabática
Si deseas obtener más información sobre estos temas o profundizar en ellos, puedes consultar las siguientes fuentes:
– [Enlace externo 1]()
– [Enlace externo 2]()
– [Enlace externo 3]()
Estos enlaces proporcionarán información adicional y más detallada sobre los conceptos y cálculos relacionados con la Mecánica de Fluidos.
Espero que este artículo te haya ayudado a comprender los diferentes tipos de flujos de fluidos y cómo calcular la descarga o velocidad de un fluido. Si tienes alguna pregunta o necesitas más ayuda, no dudes en dejar un comentario a continuación. Estaré encantado de ayudarte.