La Ecuación de movimiento de Euler y la ecuación de Bernoulli son dos elementos fundamentales en la dinámica de fluidos. Estas ecuaciones nos permiten comprender y predecir el comportamiento de los fluidos en movimiento, desde la velocidad y presión hasta la energía cinética y potencial. En este artículo, exploraremos en detalle cada una de estas ecuaciones y cómo se aplican en el estudio de los fluidos. ¡Prepárate para sumergirte en el fascinante mundo de la dinámica de fluidos y descubrir cómo estas ecuaciones pueden revelar secretos ocultos en el movimiento de los líquidos y gases!
En el artículo anterior analizamos la velocidad y la aceleración en un punto de un flujo de fluido sin considerar las fuerzas que causan el flujo. En este artículo, estudiamos el comportamiento del flujo de fluido debido a las fuerzas ejercidas por la gravedad y la presión utilizando la ecuación de movimiento de Euler.

Ecuación de movimiento del flujo de fluido.
Estudio de la dinámica del flujo de fluidos, considerando las fuerzas que provocan el flujo, mediante el análisis de la segunda ley del movimiento de Newton, que relaciona la aceleración con las fuerzas. Se supone que el fluido es incompresible y no viscoso.
Según la segunda ley del movimiento de Newton, la fuerza neta es “FX‘que actúa sobre un elemento fluido en la dirección ‘x’ es igual a la masa ‘m’ del elemento fluido multiplicada por la aceleración ‘aX‘ en dirección X.
Así que matemáticamente hablando
FX = metro × unX
….. Ecuación (a)
En el flujo de fluido actúan varias fuerzas, que se mencionan a continuación.
- FGRAMO = Gravedad.
- FPAG = la fuerza de presión
- Fv = fuerza debida a la viscosidad
- Ft = fuerza debida a la turbulencia
- FC = fuerza debida a la compresibilidad
Por favor habilite JavaScript
Por tanto, en la ecuación (a) es la fuerza neta
FX = (FGRAMO)X + (FPAG)X + (Fv)X + (Ft)X + (FC)X
- Si la fuerza debida a la compresibilidad, FC es insignificante, la fuerza neta resultante
FX = (FGRAMO)X + (FPAG)X + (Fv)X + (Ft)X
y las ecuaciones de movimiento se llaman Ecuaciones de Reynolds el movimiento. - Para flujo, donde (Ft) es insignificante, las ecuaciones de movimiento resultantes se denominan ecuación de Navier-Stokes.
- Si se supone que el flujo es ideal, la fuerza viscosa (Fv) es cero y la ecuación de movimiento se llama La ecuación de movimiento de Euler..
Ecuación de Euler del movimiento del flujo de fluido.
La ecuación de movimiento de Euler tiene en cuenta las fuerzas debidas a la gravedad y la presión.
Esta ecuación euleriana de movimiento se deriva considerando el movimiento de un elemento fluido a lo largo de una línea de corriente.
Considere una línea de corriente donde el flujo está en la dirección S, como se muestra a continuación.
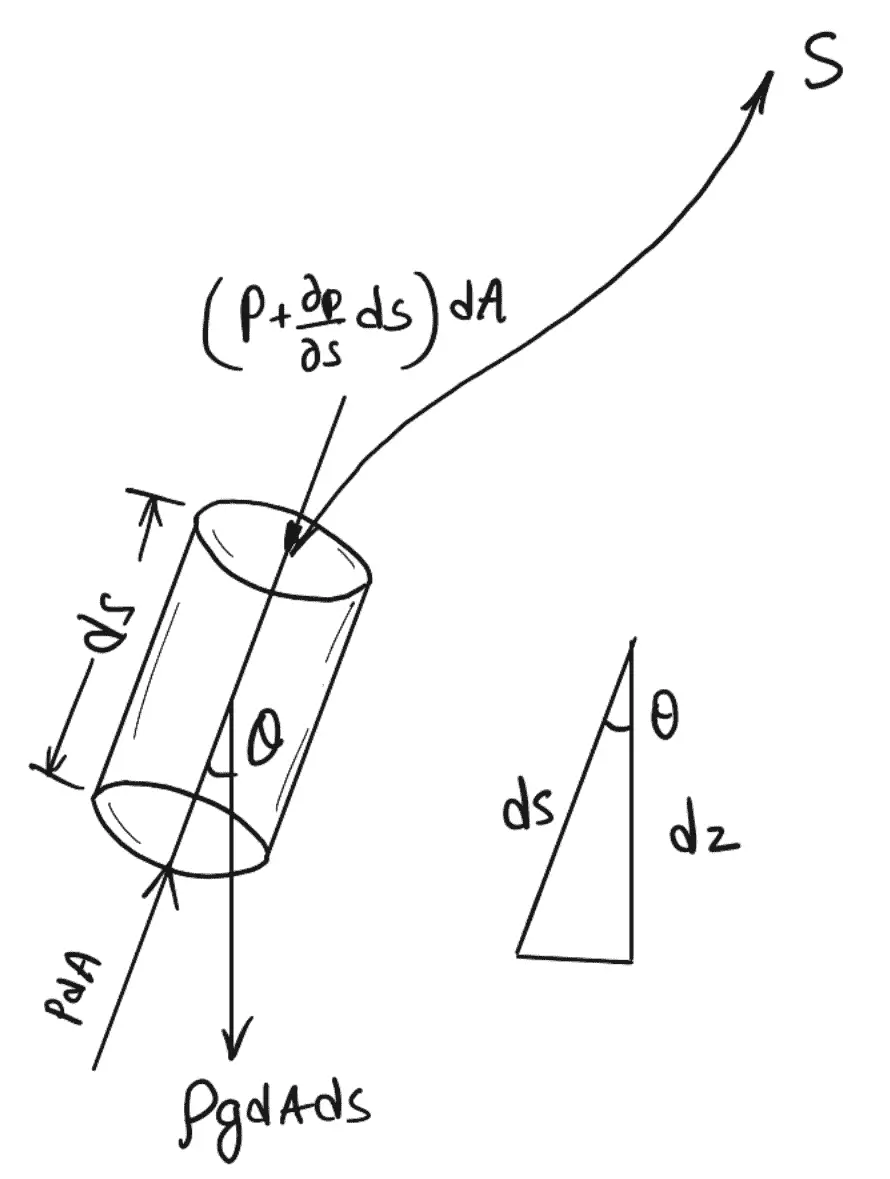
Consideremos ahora el elemento cilíndrico con sección transversal dA y longitud ds.
Las fuerzas que actúan sobre el elemento cilíndrico son las siguientes.
- fuerza de presión, pdaen la dirección del flujo.
- fuerza de presión, [p + (∂p/∂s) ds] allá en contra de la dirección del flujo.
- Peso del artículo ρgdAnuncios.
Sea θ el ángulo entre la dirección del flujo y la línea de acción del peso del elemento.
La fuerza resultante sobre el elemento fluido en la dirección «s» debe ser igual a la masa del elemento fluido × aceleración en la dirección s.
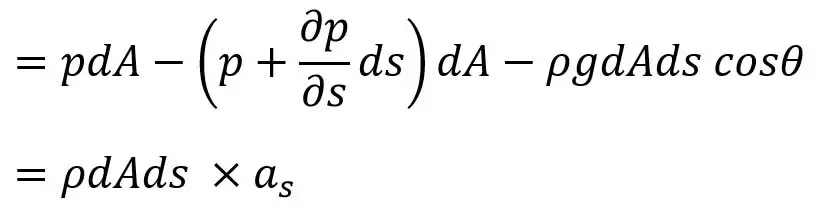
Dónde
AS = la aceleración en la dirección s.
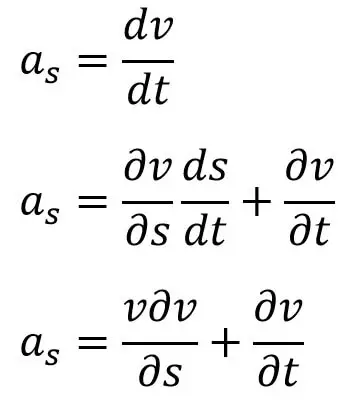
Cuando el flujo es entonces estable
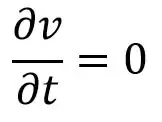
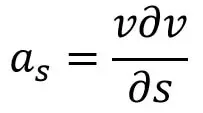
Reemplazar el valor de unS en la ecuación (b) y simplificando obtenemos
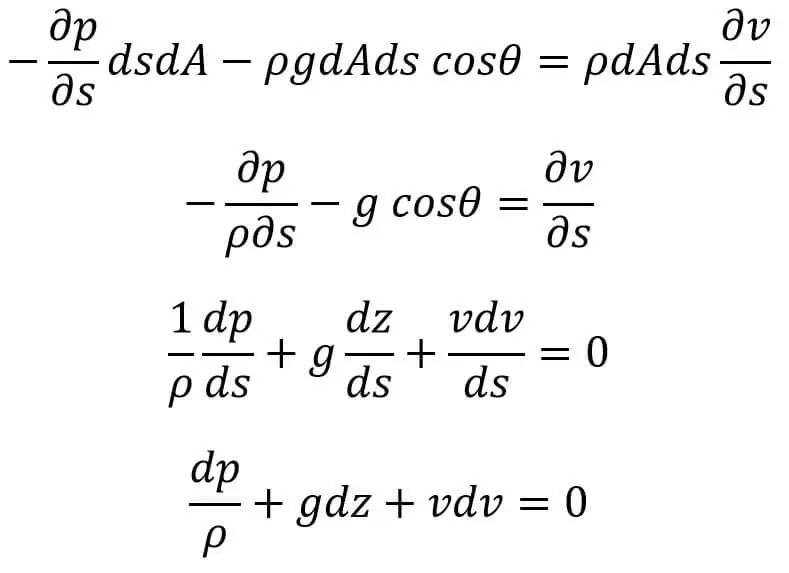
Esta es la ecuación de movimiento de Euler.
Si integramos esta ecuación de movimiento euleriana, obtenemos la ecuación de movimiento de Bernoullian.
La ecuación de movimiento de Bernoulli.
El principio de Bernoulli establece que a medida que aumenta la velocidad de un fluido en movimiento (líquido o gas), la presión dentro del fluido disminuye.
La ecuación de Bernoulli se puede obtener integrando la ecuación de movimiento de Euler (c).
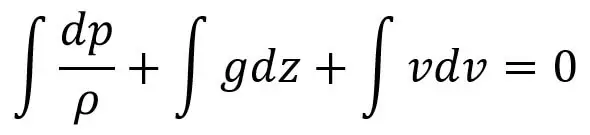
Si el flujo es incompresible, ρ es constante y
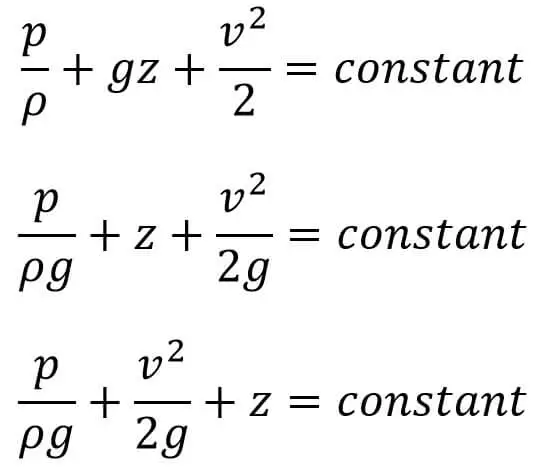
Esta es la ecuación de movimiento de Bernoulli.
Dónde
p/ρg = energía de presión por unidad de peso de líquido o altura de presión.
v2/2g = energía cinética por unidad de peso o cabeza cinética
z = Energía potencial por unidad de peso o cabeza potencial
Supuestos para la ecuación de movimiento de Bernoulli
A continuación se muestran los supuestos hechos al derivar la ecuación de Bernoulli.
(i) El líquido es ideal (la viscosidad es cero)
(ii) El flujo es constante
(iii) El flujo es incompresible
(iv) El flujo no tiene rotación.
Ecuación de movimiento de Bernoulli de un fluido real
La ecuación de Bernoulli se derivó asumiendo que el fluido no es viscoso (no viscoso) y, por lo tanto, no tiene fricción. Pero todos los líquidos reales son viscosos y, por tanto, ofrecen resistencia al flujo. Por lo tanto, siempre hay algunas pérdidas en los flujos de fluidos y por tanto estas pérdidas deben tenerse en cuenta al aplicar la ecuación de Bernoulli.
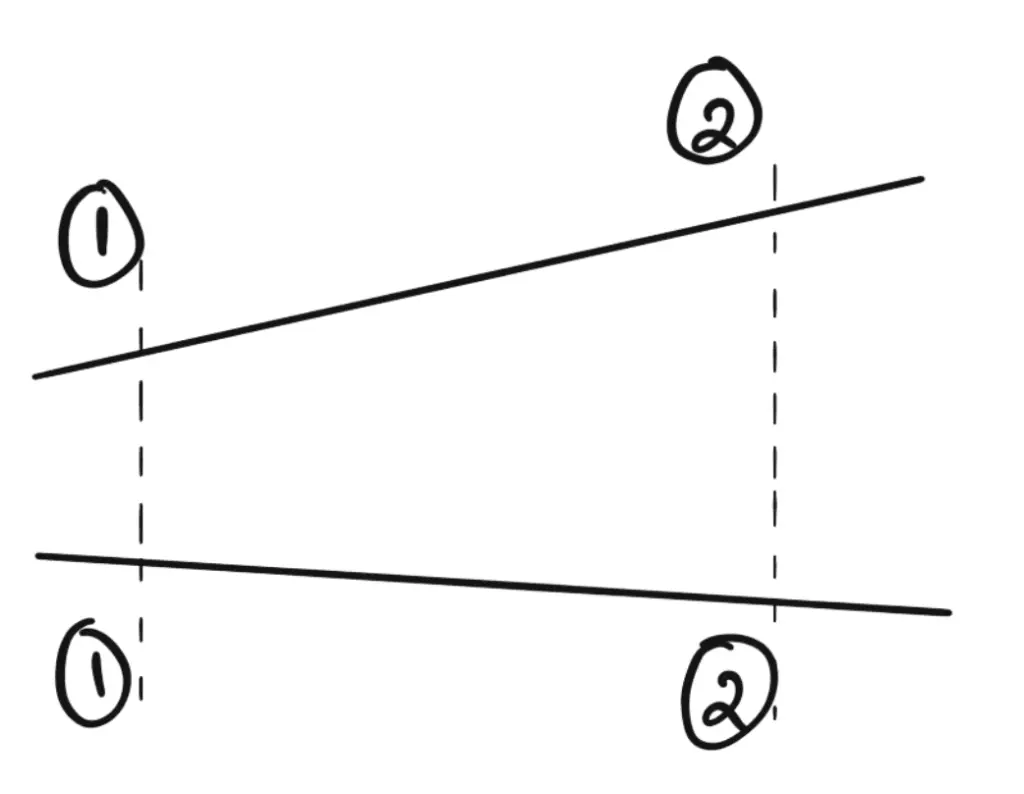
Por tanto, la ecuación de Bernoulli para fluidos reales entre los puntos 1 y 2 viene dada por
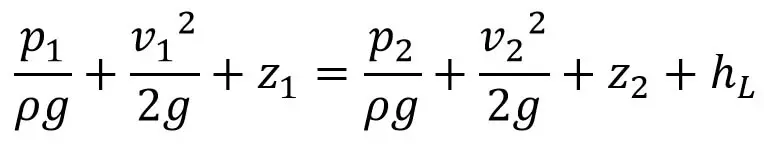
Donde Hl es la pérdida de energía entre los puntos 1 y 2
Aplicaciones de la ecuación de movimiento de Bernoulli
La ecuación de Bernoulli ahora se aplica a todos los problemas de fluidos incompresibles que involucran consideraciones de energía. Pero consideraremos su aplicación a los siguientes dispositivos de medición:
- Venturímetro
- medidor de apertura
- tubo de pitot
Se trata de la ecuación de movimiento de Bernoulli, que se deriva de la ecuación de movimiento de Euler. Háganos saber lo que piensa al respecto en la sección de comentarios a continuación.
[automatic_youtube_gallery type=»search» search=» Ecuación de movimiento de Euler en dinámica de fluidos | ecuación de Bernoulli
» limit=»1″]
Ecuación de movimiento del flujo de fluido
En el artículo anterior, discutimos la velocidad y aceleración en un punto del flujo de un fluido, sin tener en cuenta las fuerzas que causan el flujo. En este artículo, estudiaremos el comportamiento del flujo de fluido debido a las fuerzas ejercidas por la gravedad y la presión con la ayuda de la Ecuación de Movimiento de Euler.
Ecuación de movimiento del flujo de fluido
Para estudiar la dinámica del flujo de fluido considerando las fuerzas que causan el flujo mediante el análisis de la segunda ley del movimiento de Newton, que relaciona la aceleración con las fuerzas. Se supone que el fluido es incompresible y no viscoso.
Según la segunda ley del movimiento de Newton, la fuerza neta ‘Fx’ que actúa sobre un elemento de fluido en la dirección ‘x’ es igual a la masa ‘m’ del elemento de fluido multiplicada por la aceleración ‘ax’ en la dirección x.
Así matemáticamente,
Fx = m × ax ….. Ecuación (a)
En el flujo de fluido, hay diferentes fuerzas presentes, las cuales se mencionaron a continuación:
Fg = fuerza de la gravedad
Fp = fuerza de la presión
Fv = fuerza debido a la viscosidad
Ft = fuerza debido a la turbulencia
Fc = fuerza debido a la compresibilidad
Si la fuerza debido a la compresibilidad, Fc, es despreciable, la fuerza neta resultante Fx = (Fg)x + (Fp)x + (Fv)x + (Ft)x y las ecuaciones de movimiento se llaman ecuaciones de movimiento de Reynolds. Para el flujo donde (Ft) es despreciable, las ecuaciones de movimiento resultantes se conocen como Ecuaciones de Navier-Stokes. Si se asume que el flujo es ideal, la fuerza viscosa (Fv) es cero y la ecuación de movimiento se conoce como la ecuación de movimiento de Euler.
Ecuación de movimiento de Euler del flujo de fluido
Con la Ecuación de Movimiento de Euler, se tienen en cuenta las fuerzas debidas a la gravedad y la presión.
Esta Ecuación de Movimiento de Euler se deriva considerando el movimiento de un elemento de fluido a lo largo de una línea de corriente.
Consideremos una línea de corriente en la que se produce el flujo en la dirección ‘s’ como se muestra a continuación.
Ahora consideremos el elemento cilíndrico de sección transversal dA y longitud ds.
Las fuerzas que actúan sobre el elemento cilíndrico son las siguientes:
Fuerza de presión, pdA, en la dirección del flujo.
Fuerza de presión, [p + (∂p/∂s) ds] dA en dirección opuesta al flujo.
Peso del elemento ρgdAds.
Sea θ el ángulo entre la dirección del flujo y la línea de acción del peso del elemento.
La fuerza resultante sobre el elemento de fluido en la dirección ‘s’ debe ser igual a la masa del elemento de fluido × aceleración en la dirección s.
Ecuación (b)
Donde as = la aceleración en la dirección de s.
Si el flujo es constante, entonces
Sustituyendo el valor de as en la ecuación (b) y simplificando, obtendremos
Ecuación (c)
Esta es la Ecuación de Movimiento de Euler.
Integrando esta Ecuación de Movimiento de Euler, obtenemos la Ecuación de Movimiento de Bernoulli.
Ecuación de movimiento de Bernoulli
El principio de Bernoulli establece que a medida que la velocidad de un fluido en movimiento aumenta (líquido o gas), la presión dentro del fluido disminuye.
La ecuación de Bernoulli se puede obtener mediante la integración de la ecuación de movimiento de Euler (c):
Si el flujo es incompresible, entonces ρ es constante y
Ecuación (d)
Esta es la Ecuación de Movimiento de Bernoulli.
Preguntas frecuentes:
- ¿Cuál es la ecuación de movimiento de Euler del flujo de fluido?
- ¿Qué fuerzas se tienen en cuenta en la ecuación de movimiento de Euler?
- ¿Qué es la ecuación de movimiento de Bernoulli?
- ¿Cuáles son las aplicaciones de la ecuación de movimiento de Bernoulli?
Esta es toda la información sobre la Ecuación de Movimiento de Bernoulli, que se deriva de la Ecuación de Movimiento de Euler. Haznos saber lo que piensas sobre esto en la sección de comentarios a continuación.
Fuentes externas:
– Wikipedia: Ecuación de Navier-Stokes
– Wikipedia: Principio de Bernoulli
