El flujo de vórtice es un fenómeno fascinante y complejo que ocurre en fluidos, tanto líquidos como gases. A simple vista, puede parecer simplemente un remolino de agua o aire, pero en realidad es mucho más que eso. Este fenómeno puede influir en diferentes aspectos, desde la meteorología hasta la aerodinámica de aviones y autos deportivos. En este artículo, exploraremos qué es el flujo de vórtice y comprendamos mejor su funcionamiento a través de la ecuación de movimiento. ¡Prepárate para adentrarte en el mundo de la física y descubrir los secretos de este interesante fenómeno!
Ya hemos discutido los diferentes tipos de flujo de fluido, analizando seis formas de determinar la velocidad y la aceleración del flujo. El flujo de vórtice se divide en flujo laminar y turbulento. El flujo de vórtice es el flujo de un líquido a lo largo de una trayectoria curva o el flujo de una masa en rotación. Un ejemplo de este tipo de flujo es el flujo de un líquido en un impulsor, un remolino en un río. Analicemos más detalles sobre el flujo de vórtice y la ecuación de movimiento del flujo de vórtice.


flujo de vórtice
Ya hemos mencionado que el flujo de vórtice se define como el flujo de un fluido a lo largo de una trayectoria curva o el flujo de una masa en rotación. En realidad, existen dos tipos diferentes de flujos de vórtice.
- Corrientes de Foucault forzadas
- Corrientes de Foucault libres
Analicemos en detalle estos dos tipos de flujos de vórtice.
Corrientes de Foucault forzadas

El vórtice forzado ahora se define como el tipo de flujo de vórtice en el que se requiere un cierto par externo para hacer girar la masa de fluido. La masa líquida en este flujo gira con una velocidad angular constante ω.
La velocidad tangencial de cualquier partícula fluida está dada por
v = ω×r
Dónde
r = radio de la partícula de fluido desde el eje de rotación
Por favor habilite JavaScript
Todos reescribimos la ecuación anterior de la siguiente manera:
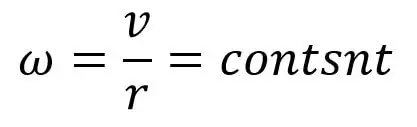
Algunos de los flujos de vórtices forzados se enumeran a continuación.
- La licuadora de jugo es el mejor ejemplo de Forced Vortex Flow que vemos todos los días como una aplicación doméstica.
- La mezcla de colores que se muestra arriba es también uno de los mejores ejemplos de flujo de vórtice forzado.
- Otro ejemplo es el flujo de fluido en el impulsor de una bomba de agua.
- El flujo de agua a través del impulsor de la turbina.
Corrientes de Foucault libres

Cuando no se requiere un par externo para hacer girar la masa de fluido, este tipo de flujo se denomina flujo de vórtice libre.
Así, en el caso del vórtice libre, el fluido gira debido a la rotación previamente impartida al fluido.
A continuación se enumeran ejemplos de flujo de vórtice libre.
- El fluido fluye a través de un agujero en el fondo de un recipiente.
- Flujo de fluido alrededor de una curva circular en la tubería.
- Un remolino en un río.
- Flujo de fluido en la carcasa de una bomba centrífuga.
La relación entre velocidad y radio en el vórtice libre se puede obtener estableciendo el valor del par externo igual a cero, o la tasa de cambio del momento angular con el tiempo. Esto significa que el impulso debe ser cero.
Considere una partícula líquida de masa “m” a una distancia radial “r” del eje de rotación con una tangencial v.
Entonces momento angular = masa × m × v
Par de impulso = impulso × r = m × v × r
Tasa de cambio temporal del momento angular = ∂/∂t (mvr)
Para vórtice libre ∂/∂t (mvr) = 0
Integramos ambos lados
mvr = constante
vr = constante/m
vr = constante
…….Ecuación (b)
Como puede ver, la aplicación de flujo de vórtice forzado y flujo de vórtice libre juega un papel importante en la aplicación de muchas aplicaciones que van desde el nivel doméstico hasta el industrial. Es muy importante estudiar el flujo y comprender la ecuación de movimiento de estos flujos de vórtice libres y forzados.
Ecuación de movimiento para el flujo de vórtice
Considere un elemento fluido ABCD (que se muestra sombreado) en la siguiente figura.
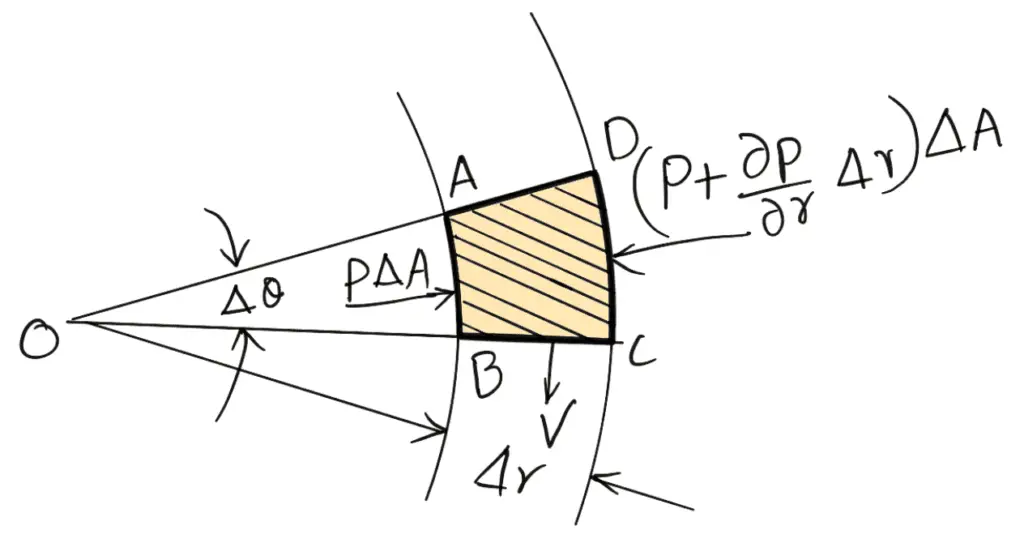
El elemento fluido gira con velocidad uniforme en un plano horizontal alrededor de un eje perpendicular al plano del papel y pasa por O.
Asumamos
r = radio del elemento de O.
Δθ = ángulo que ocupa el elemento en O.
Δr Espesor radial del elemento.
ΔA = área de la sección transversal del elemento Δ.
Las fuerzas que actúan sobre el elemento son:
- Fuerza de compresión, pΔA, sobre la superficie AB.
- fuerza de presión, [p + (∂p/∂r) Δr] ΔA en el CD frontal.
- fuerza centrífuga, mv2/r actúa en dirección opuesta al centro O.
La masa del elemento = densidad de masa × volumen
metro = ρ × ΔA × Δr
Fuerza centrífuga = ρ × ΔA × Δr v2/R
Igualemos las fuerzas en la dirección radial. obtenemos lo siguiente
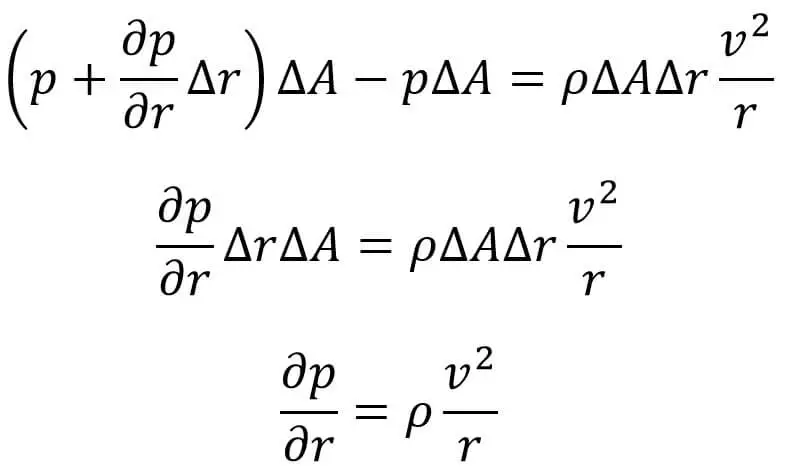
La ecuación (c) proporciona la variación de presión a lo largo de la dirección radial para un flujo de vórtice libre o forzado en un plano horizontal.
La expresion ∂p/∂r se llama gradiente de presión en la dirección radial.
Como ∂p/∂r es positivo, por lo tanto la presión aumenta a medida que aumenta el radio “r”.
La fluctuación de presión en el plano vertical resulta de la ley hidrostática de la siguiente manera:
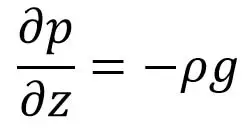
En la ecuación (d) anterior, “z” se mide verticalmente en dirección ascendente.
La presión «p» varía con respecto a «r» y «z» o «p» es función de «r» y «z». por lo tanto la derivada total de ‘p’ se convierte en
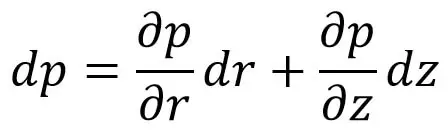
Sustituyamos la ecuación (c) y la ecuación (d), y la expresión anterior es la siguiente:
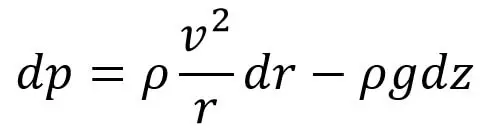
Esta ecuación (e) da la variación de presión del fluido en rotación en cada plano. Esta es la ecuación de movimiento de la corriente parásita.
Ecuación de flujo de vórtice forzado
Como mencionamos anteriormente, la velocidad tangencial de cada partícula de fluido está dada por
v = ω×r
Dónde
ω = velocidad angular = constante
r = radio de la partícula de fluido desde el eje de rotación
y tenemos la ecuación de movimiento para el flujo del vórtice desde arriba
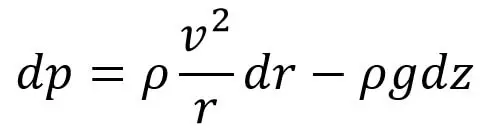
Sustituyendo el valor de v en esta ecuación, obtenemos:
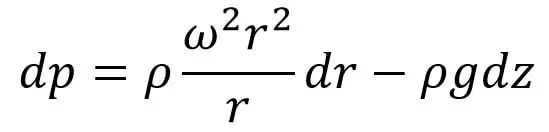
Consideremos dos puntos (1 y 2) del fluido, como se muestra en la siguiente figura, donde hay un flujo de vórtice forzado.
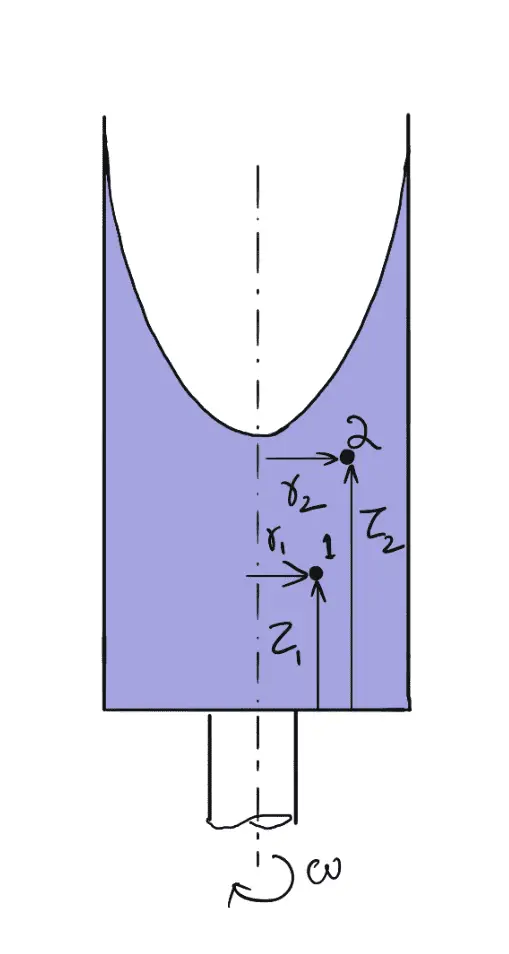
Si integramos la ecuación anterior para los puntos 1 y 2, obtenemos:
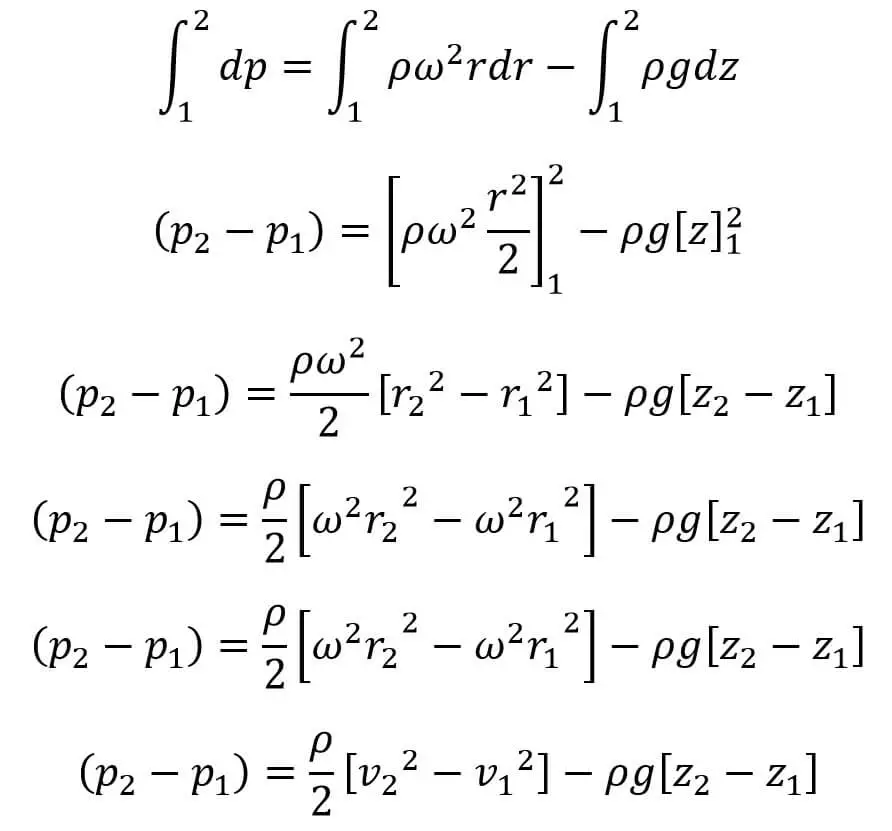
Si estos dos puntos 1 y 2 se encuentran en la superficie libre del líquido como se muestra en la siguiente figura.
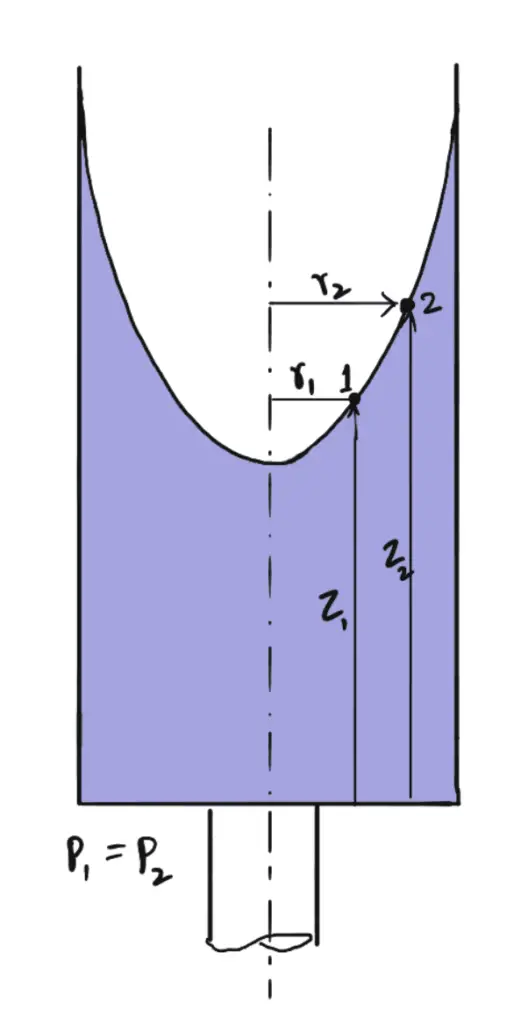
Si los dos puntos 1 y 2 se encuentran en la superficie libre, entonces la p1 =S2 entonces la ecuación anterior resulta
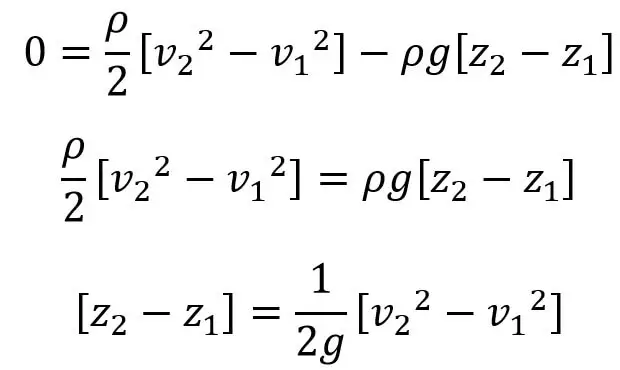
Si el punto 1 está en el eje de rotación, entonces se aplica v1 = ω×r1 = ω × 0 = 0
La ecuación anterior se puede escribir de la siguiente manera
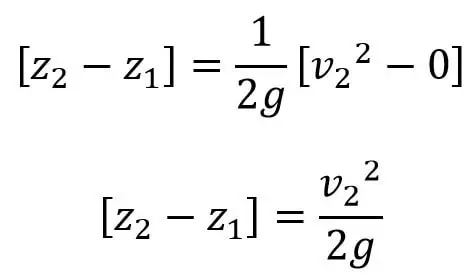
Por ejemplo, dejemos2 – p.ej1 = Z, entonces podemos escribir la ecuación anterior
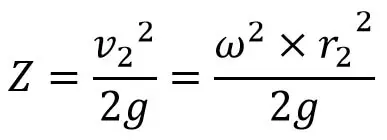
Por tanto, Z varía con el cuadrado de r. Por lo tanto, la ecuación (f) es una ecuación paraboloide.
Se trata de la ecuación de movimiento para el flujo de vórtice y el flujo de vórtice forzado. Háganos saber lo que piensa al respecto en la sección de comentarios a continuación.
[automatic_youtube_gallery type=»search» search=» ¿Qué es el flujo de vórtice? | Ecuación de movimiento del flujo de vórtice.
» limit=»1″]
Flujo Vortex: Tipos y Ecuación de Movimiento
Flujo Vortex
Ya hemos mencionado que el flujo vortex se define como el flujo de un fluido a lo largo de una trayectoria curva o el flujo de una masa en rotación. De hecho, existen dos tipos diferentes de flujos vortex.
Flujo Vortex Forzado: Requiere un torque externo para rotar la masa de fluido.
Flujo Vortex Libre: No requiere torque externo para rotar la masa de fluido.
Discutiremos estos dos tipos de flujos vortex de manera detallada.
Flujo Vortex Forzado
Un ejemplo de flujo vortex forzado es el mezclador de pintura. Este tipo de flujo vortex requiere de un torque externo para girar la masa de fluido a una velocidad angular constante, ω.
La velocidad tangencial de cualquier partícula de fluido se calcula mediante la fórmula
v = ω × r
Donde:
r = radio de la partícula de fluido con respecto al eje de rotación
Podemos reescribir la ecuación anterior de la siguiente manera:
Ecuación (a)
Algunos ejemplos de flujo vortex forzado son:
– El mezclador de jugo, un ejemplo común que vemos en aplicaciones domésticas.
– La mezcla de pinturas, como se muestra arriba, también es un ejemplo de flujo vortex forzado.
– El flujo de fluido dentro del impulsor de una bomba de agua.
– El flujo de agua a través de la rueda de una turbina.
Flujo Vortex Libre
Un ejemplo de flujo vortex libre es el remolino en un río. En este tipo de flujo, no se requiere un torque externo para rotar la masa de fluido. En cambio, el líquido rota debido a la rotación que se le ha impartido previamente.
Algunos ejemplos de flujo vortex libre son:
– El flujo de líquido a través de un agujero en la parte inferior de un recipiente.
– El flujo de líquido alrededor de una curva circular en una tubería.
– El remolino en un río.
– El flujo de fluido en la carcasa de una bomba centrífuga.
La relación entre la velocidad y el radio en el flujo vortex libre se puede obtener al igualar el valor del torque externo a cero, lo que implica que el momento angular debe ser cero.
Consideremos una partícula de fluido de masa ‘m’ a una distancia radial ‘r’ del eje de rotación, con una velocidad tangencial ‘v’.
Entonces, el momento angular = Masa × m × v
El momento de momento = Momento × r = m × v × r
La tasa de cambio del momento angular = ∂/∂t (m v r)
Para el flujo vortex libre ∂/∂t (mvr) = 0
Integrando en ambos lados obtendremos:
mvr = Constantevr = Constante/mvr = Constante
…….Ecuación (b)
Como puedes ver, la aplicación del flujo vortex forzado y el flujo vortex libre tiene un papel importante en diversas aplicaciones, desde el ámbito doméstico hasta el industrial. Es muy importante estudiar el flujo y comprender la ecuación de movimiento para estos tipos de flujos vortex.
Ecuación de Movimiento para el Flujo Vortex
Consideremos un elemento de fluido ABCD (mostrado sombreado) en la siguiente figura.
El elemento de fluido rota a una velocidad uniforme en un plano horizontal alrededor de un eje perpendicular al plano del papel y que pasa por O.
Supongamos que:
r = Radio del elemento con respecto a O.
Δθ = Ángulo subtendido por el elemento en O.
Δr = Espesor radial del elemento.
ΔA = Área de la sección transversal del elemento Δ.
Las fuerzas que actúan sobre el elemento son:
– Fuerza de presión, pΔA, en la cara AB.
– Fuerza de presión, [p + (∂p/∂r) Δr] ΔA en la cara CD.
– Fuerza centrífuga, mv2/r actuando en dirección opuesta al centro O.
La masa del elemento se calcula como: masa = densidad del fluido × volumen
m = ρ × ΔA × Δr
Fuerza centrífuga = ρ × ΔA × Δr v2/r
Igualando las fuerzas en dirección radial, obtenemos la siguiente ecuación:
Ecuación (c)
La ecuación (c) proporciona la variación de presión a lo largo de la dirección radial para un flujo vortex forzado o vortex libre en un plano horizontal.
La expresión ∂p/∂r se llama gradiente de presión en la dirección radial.
Como ∂p/∂r es positivo, esto implica que la presión aumenta con el aumento del radio ‘r’.
La variación de presión en el plano vertical se rige por la ley hidrostática, que se expresa de la siguiente manera:
Ecuación (d)
En la ecuación (d), ‘z’ se mide verticalmente en dirección ascendente.
La presión ‘p’ varía con respecto a ‘r’ y ‘z’, es decir, ‘p’ es una función de ‘r’ y ‘z’. Por lo tanto, la derivada total de ‘p’ se convierte en:
Ecuación (e)
La ecuación (e) proporciona la variación de presión en un fluido en rotación en cualquier plano. Esta es la ecuación de movimiento para el flujo vortex.
Ecuación del Flujo Vortex Forzado
Como mencionamos anteriormente, la velocidad tangencial de cualquier partícula de fluido se calcula mediante la fórmula v = ω × r, donde ω es velocidad angular constante y r es el radio de la partícula de fluido con respecto al eje de rotación.
Teniendo en cuenta la ecuación de movimiento para el flujo vortex, podemos reemplazar el valor de ‘v’ en la misma y obtener lo siguiente:
Consideremos dos puntos (1 y 2) del fluido como se muestra en la siguiente figura, donde hay flujo vortex forzado.
Integrando la ecuación anterior para los puntos 1 y 2 obtenemos:
Si estos dos puntos 1 y 2 están en la superficie libre del fluido como se muestra en la siguiente figura:
Si los puntos 1 y 2 están en la superficie libre, entonces p1 = p2, y la ecuación anterior se convierte en:
Si el punto 1 está en el eje de rotación, entonces v1 = ω × r1 = ω × 0 = 0
La ecuación anterior se puede escribir de la siguiente manera:
Si z2 – z1 = Z, entonces podemos escribir la ecuación anterior como:
Por lo tanto, Z varía con el cuadrado de r. Por lo tanto, la ecuación (f) es una ecuación de un paraboloide.
Esto es todo sobre la ecuación de movimiento para el flujo vortex y el flujo vortex forzado. Cuéntanos qué opinas sobre esto en la sección de comentarios a continuación.
- ¿Cuáles son los dos tipos de flujo vortex discutidos en este artículo?
- ¿Cuál es la definición de flujo vortex forzado?
- ¿Qué es el flujo vortex libre y cuál es un ejemplo de este tipo de flujo?
- ¿Cuál es la ecuación de movimiento para el flujo vortex?
- ¿Cuál es la relación entre la presión y el radio en el flujo vortex?
Lea más sobre flujo vortex y su aplicación en diferentes industrias aquí.
