Velocidad y aceleración de un flujo de fluido.

¿Qué tan rápido fluye un fluido? ¿Cómo se puede medir su velocidad y aceleración? Estas preguntas son fundamentales para comprender el comportamiento de los fluidos en diferentes situaciones. En este artículo, exploraremos el fascinante mundo de la velocidad y aceleración de un flujo de fluido. Descubriremos las diferencias entre ambos conceptos y cómo se relacionan entre sí. También exploraremos las diversas formas de medir y calcular estos parámetros, proporcionando ejemplos prácticos y aplicaciones en la vida cotidiana. Sin duda, adentrarse en el estudio de la velocidad y aceleración de un flujo de fluido nos permitirá comprender mejor el funcionamiento de nuestro entorno. ¡Así que prepárate para sumergirte en esta apasionante aventura científica!

En el artículo anterior, analizamos los tipos de flujo de fluido, descarga de fluido (Q) y las ecuaciones de continuidad para un flujo de fluido. A partir de los tipos de flujo de fluido, podemos determinar fácilmente los componentes de velocidad y aceleración del flujo de fluido.

velocidad

En mecánica de fluidos, la velocidad se define como el cambio de posición en el tiempo o el desplazamiento del fluido en la unidad de tiempo. La velocidad es una cantidad vectorial.

Por lo tanto, los componentes de la velocidad son función de las coordenadas espaciales (es decir, la longitud de la dirección del flujo) y del tiempo.

Ahora consideremos que u, v y w son las componentes en las direcciones x, y y z. y t es el componente de tiempo.

Matemáticamente, las componentes de la velocidad se pueden escribir de la siguiente manera:

tu = f₁(x, y, z, t)
v = f₂(x, y, z, t)
w = f₃(x, y, z, t)

Sea V la velocidad resultante en cualquier punto de un flujo de fluido, entonces podemos escribirla de la siguiente manera:

V = ui + vj + semana

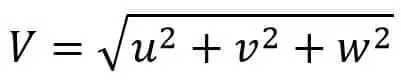
Esta es la velocidad resultante en cualquier punto de un flujo de fluido.

aceleración

En mecánica de fluidos, la aceleración se define como la tasa de cambio del flujo de fluido en relación con el tiempo. La aceleración es una cantidad vectorial.

Supongamos un_X A_j y un_p.ej son la aceleración total en las direcciones xy y z, respectivamente.

Entonces podemos escribir usando la regla de la cadena de diferenciación.

Para un flujo constante sabemos

∂V/∂t = 0

donde V es la velocidad resultante.

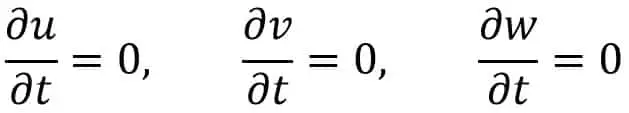
Por lo tanto, la aceleración en las direcciones x, y y z se puede escribir como

Ecuación (b)

El vector de aceleración

Una = una_Xyo + un_jj+a_p.ejk

Aceleración local y aceleración convectiva.

aceleración local se define como la tasa de aumento de la velocidad a lo largo del tiempo en un punto dado en un campo de flujo.

En la ecuación (a), la siguiente expresión se llama aceleración local.

aceleración convectiva se define como la tasa de cambio de velocidad debido al cambio de posición de las partículas de un fluido en una corriente de fluido.

Las expresiones distintas de la siguiente parte de la ecuación (a) se denominan aceleración convectiva.

Tareas de ejemplo para calcular la velocidad y aceleración de una partícula líquida.

Planteamiento del problema: El vector de velocidad en un flujo de fluido viene dado de la siguiente manera
V = (4x³)yo – (10x²y)j + (2t)k
Encuentre la velocidad y aceleración de una partícula fluida en (2, 1, 3) en el tiempo t = 1.

Respuesta:

velocidad

Las componentes de la velocidad son u, v y w.
tu = (4x³)
v = -(10x²y)
w = (2t)

Desde el punto (2, 1, 3) tenemos x = 2, y = 1 y z=3 en el instante t = 1.

Por tanto, las componentes de la velocidad son (2, 1, 3).

tu = (4×2³) = 32 unidades
v = -(10×2²×1) = -40 unidades
w = (2×1) = 2 unidades

El vector velocidad V en (2, 1, 3)

V = (32)i – (40)j + (2)k

La velocidad resultante será

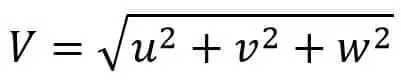
V = √[(32)² + (-40)² + (2)²]
V = √[1024+1600+4]
V = 51,26 unidades

aceleración

Conocemos la ecuación de aceleración.

De los componentes de velocidad ahora podemos escribir:

Reemplazar los valores da como resultado los componentes de la aceleración en (2, 1, 3) en el tiempo t = 1

A_X = (4x³) × (12x²) + (-10x²y) × (0) + (2t) × (0) + 0
= 48x⁵
= 48(2)⁵
A_X = 1536 unidades

A_j = (4x³) × (-20xy) + (-10x²y) × (-10x²) + (2t) × (0) + 0
= -80x⁴+100x⁴j
= -80(2)⁴(1) +100(2)⁴(1)
A_j = 320 unidades

A_p.ej = (4x³) × (0) + (-10x²y) × (0) + (2t) × (0) + 2,1
A_p.ej = 1536 unidades

La aceleración es A = a_Xyo + un_jj+a_p.ejk

A = 1536i +320j + 2k

La aceleración resultante es

Una = √[(1536)² + (320)² + (2)²]
Una = √[2359296+102400+4]
A = 1569 unidades

Esto le permite calcular la velocidad y la aceleración de cualquier partícula de fluido a partir de la ecuación del vector de velocidad dada.

Háganos saber lo que piensa sobre este artículo en la sección de comentarios a continuación.

[automatic_youtube_gallery type=»search» search=»Velocidad y aceleración de un flujo de fluido.

» limit=»1″]

Velocidad

En la mecánica de fluidos, la velocidad se define como el cambio de posición con respecto al tiempo o el desplazamiento del fluido en unidad de tiempo. La velocidad es una cantidad vectorial.

Las componentes de la velocidad son una función de las coordenadas espaciales (es decir, longitud de dirección del flujo) y el tiempo.

Ahora consideremos u, v y w como las componentes en las direcciones x, y y z, respectivamente, y t como la componente de tiempo.

Matemáticamente, las componentes de velocidad se pueden escribir de la siguiente manera:

• u = f1(x, y, z, t)
• v = f2(x, y, z, t)
• w = f3(x, y, z, t)

Si V es la velocidad resultante en cualquier punto de un flujo de fluido, entonces podemos escribirlo de la siguiente manera:

V = ui + vj + wk

Esta es la velocidad resultante en cualquier punto de un flujo de fluido.

Aceleración

En la mecánica de fluidos, la aceleración se define como la tasa de cambio de la velocidad del flujo de fluido con respecto al tiempo. La aceleración es una cantidad vectorial.

Supongamos que ax, ay y az son las aceleraciones totales en las direcciones x, y y z, respectivamente. Luego, utilizando la regla de la cadena de la diferenciación, podemos escribir:
Equation (a)

Para flujo estable, sabemos que:
∂V/∂t = 0

donde V es la velocidad resultante.

Por lo tanto, la aceleración en las direcciones x, y y z se puede escribir como:

Equation (b)
El vector de aceleración

A = axi + ayj + azk

Equation (c)

Aceleración local y aceleración convectiva

La aceleración local se define como la tasa de aumento de la velocidad con respecto al tiempo en un punto dado en un campo de flujo.
En la ecuación dada por (a), la siguiente expresión se conoce como aceleración local.

La aceleración convectiva se define como la tasa de cambio de la velocidad debido al cambio de posición de las partículas de fluido en un flujo de fluido.

Las expresiones aparte de la siguiente parte en la ecuación (a) se conocen como aceleración convectiva.

Ejemplos de problemas para calcular la velocidad y aceleración de una partícula de fluido

Enunciado del problema: El vector de velocidad en un flujo de fluido se da de la siguiente manera: V = (4×3)i – (10x2y)j + (2t)k. Encuentra la velocidad y aceleración de una partícula de fluido en (2, 1, 3) en el momento t = 1.

Respuesta:
Velocidad
Las componentes de velocidad u, v y w son:
u = (4×3)
v = -(10x2y)
w = (2t)

Desde el punto (2, 1, 3), tenemos x = 2, y = 1 y z = 3 en el momento t = 1.
Por lo tanto, las componentes de velocidad (2, 1, 3) son:
u = (4×23) = 32 unidades
v = -(10×22×1) = -40 unidades
w = (2×1) = 2 unidades

El vector de velocidad V en (2, 1, 3) es:

V = (32)i – (40)j + (2)k
La velocidad resultante será:
V = √[(32)2 + (-40)2 + (2)2]
V = √[1024+1600+4]
V = 51.26 unidades

Aceleración
La ecuación de aceleración que conocemos es:

Ahora, a partir de las componentes de velocidad, podemos escribir:

Sustituyendo los valores, las componentes de aceleración en (2, 1, 3) en el momento t = 1 son:

ax = (4×3) × (12×2) + (-10x2y) × (0) + (2t) × (0) + 0
= 48×5
= 48(2)5
ax = 1536 unidades

ay = (4×3) × (-20xy) + (-10x2y) × (-10×2) + (2t) × (0) + 0
= -80x4y + 100x4y
= -80(2)4(1) + 100(2)4(1)
ay = 320 unidades

az = (4×3) × (0) + (-10x2y) × (0) + (2t) × (0) + 2.1
az = 1536 unidades

La aceleración es A = axi + ayj + azk

A = 1536i + 320j + 2k
La aceleración resultante es:
A = √[(1536)2 + (320)2 + (2)2]
A = √[2359296+102400+4]
A = 1569 unidades

Así es como puedes calcular la velocidad y aceleración de cualquier partícula de fluido a partir de la ecuación del vector de velocidad dada.

Preguntas frecuentes

1. ¿Qué es la velocidad en la mecánica de fluidos?
2. ¿Cómo se calculan las componentes de velocidad?
3. ¿Qué es la aceleración en la mecánica de fluidos?
4. ¿Cuál es la ecuación de aceleración para un flujo estable?

Por favor, déjanos saber tu opinión sobre este artículo en la sección de comentarios a continuación.

Para obtener más información sobre mecánica de fluidos, consulta los siguientes enlaces externos:
– [Enlace 1](https://www.ejemplode.com/ejemplo/36/fluidos__mecanica_de_los_fluidos:_tipos_de_flujo.html)
– [Enlace 2](https://www.ejemplode.com/ejemplo/36/fluidos__mecanica_de_los_fluidos:_teorema_de_la_resultante_de_un_sistema_de_fuerzas.html)