¿Alguna vez has querido entender cómo se calculan los índices de Miller para los planos cristalográficos? ¡Estás en el lugar correcto! En este artículo, te explicaremos de manera sencilla y concisa cómo puedes calcular estos índices, dándote las herramientas necesarias para comprender la estructura de los cristales de una manera fascinante. Prepara tu mente curiosa y adéntrate en el mundo de la cristalografía. ¡Comencemos!
A veces es necesario hacer referencia a planos reticulares específicos de átomos dentro de una estructura cristalina, o puede ser de interés conocer la orientación cristalográfica de un plano o grupo de planos en una red cristalina. Para identificar planos cristalinos en estructuras cristalinas cúbicas o hexagonales, se utiliza el sistema de notación de Miller. Veamos cómo podemos calcular los índices de Miller para planos cristalográficos en el sistema cúbico y la estructura cristalina hexagonal.


Índices de Miller para niveles cristalográficos.
Los índices de Miller de un plano cristalino se definen como los recíprocos de las intersecciones fraccionarias (con fracturas limpias) que el plano forma con los ejes cristalográficos x, y y z de los tres bordes no paralelos de la celda unitaria cúbica.
Las aristas del cubo de la celda unitaria representan longitudes unitarias, y las intersecciones de los planos de la red se miden utilizando estas longitudes unitarias.
Método para determinar los índices de Miller para el plano cristalino cúbico.
El procedimiento para determinar los índices de Miller para un plano cristalino cúbico es el siguiente:
- Seleccione un plano que no pase por el origen en (0, 0, 0).
- Determine las intersecciones de los planos utilizando los ejes cristalográficos x, y y z para un cubo unitario. Estas secciones pueden ser fracciones.
- Encuentra los recíprocos de estas secciones.
- Elimina fracciones y encuentra el conjunto más pequeño de números enteros que tengan la misma proporción que las intersecciones. Estos números enteros son los índices de Miller del plano cristalográfico y se colocan entre paréntesis sin comas. La notación (hkl) se utiliza para indicar índices de Miller en el sentido general, donde h, k y l son los índices de Miller de un plano cristalino cúbico para los ejes x, y y z, respectivamente.
La siguiente figura muestra tres de los principales niveles cristalográficos de estructuras cristalinas cúbicas.
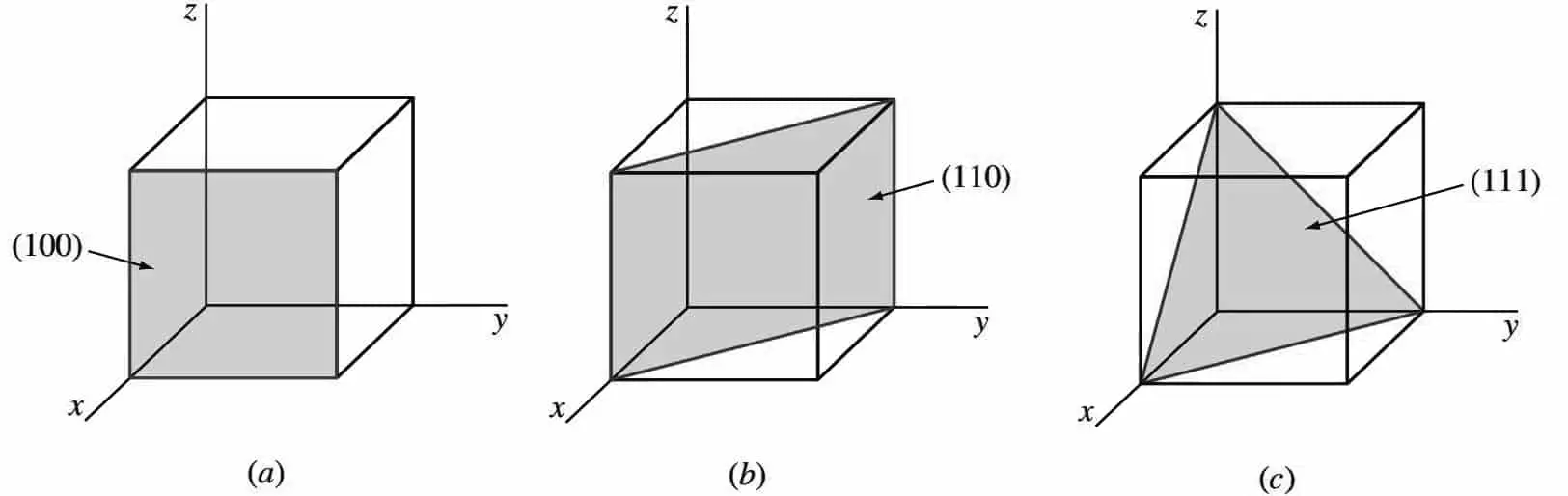
- Consideremos primero el plano cristalino sombreado en la figura a, que tiene intersecciones 1, ∞, ∞ para los ejes x, y y z, respectivamente.
- Tomamos los recíprocos de estas intersecciones para obtener los índices de Miller, que son 1, 0, 0.
- Como estos números no implican fracciones, los índices de Miller para este plano son (100), que se lee como el plano uno-cero-cero.
- A continuación, veamos el segundo nivel, que se muestra en la figura b. Las intersecciones de este plano son 1, 1, ∞.
- Como los recíprocos de estos números son 1, 1, 0, que no son fracciones, los índices de Miller de este nivel son (110).
- Finalmente, el tercer nivel en la figura c tiene las intersecciones 1, 1, 1, que dan los índices de Miller (111) para este nivel.
Ahora consideremos el plano cristalino cúbico que se muestra en la siguiente figura, cuyo eje intercepta 1/3, 2/3, 1.
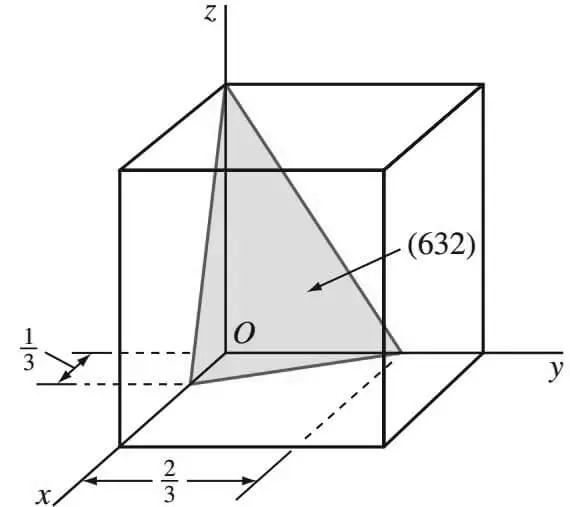
- Los recíprocos de estas secciones son 3, 3/2, 1.
- Dado que no se permiten secciones fraccionarias, estas secciones fraccionarias deben multiplicarse por 2 para eliminar las fracciones 3/2.
- Por tanto, las intersecciones recíprocas se convierten en 6, 3, 2 y los índices de Miller son (6 3 2).
- En el problema de ejemplo siguiente se analizan ejemplos adicionales de planos de cristal cúbico.
- Si el plano cristalino en consideración pasa por el origen de modo que uno o más puntos de intersección son cero, el plano debe trasladarse a una posición equivalente en la misma celda unitaria y el plano debe permanecer paralelo al plano original.
- Esto es posible porque todos los planos paralelos a la misma distancia se caracterizan por los mismos índices de Miller.
- Cuando conjuntos de planos reticulares equivalentes están unidos entre sí por la simetría del sistema cristalino, se denominan planos de una familia o forma, y los índices de un plano de la familia se incluyen entre llaves como {hkl} para representar los índices de una familia de planos simétricos.
Por ejemplo, los índices de Miller de los planos de superficie cúbicos (100), (010) y (001) se denominan colectivamente familia o forma mediante la notación {100}.
Por favor habilite JavaScript
Veamos un problema de ejemplo para dibujar los planos cristalográficos en celdas unitarias cúbicas.
Problema de ejemplo sobre niveles cristalográficos en celdas unitarias cúbicas
Dibuje los siguientes planos cristalográficos en celdas unitarias cúbicas:
R. (1 0 1)
B. (1 1̄ 0)
C. (2 2 1)
D. Dibuje un plano (1 1 0) en una celda unitaria BCC que contenga ubicaciones de átomos y enumere las coordenadas de posición de los átomos cuyos centros son intersecados por este plano.
Respuesta:
R. (1 0 1)
Primero determine los recíprocos de los índices de Miller del plano (1 0 1).
Estos son 1, ∞, 1. El plano (1 0 1) debe pasar por un cubo unitario en las intersecciones x = 1 y z = 1 y ser paralelo al eje y.
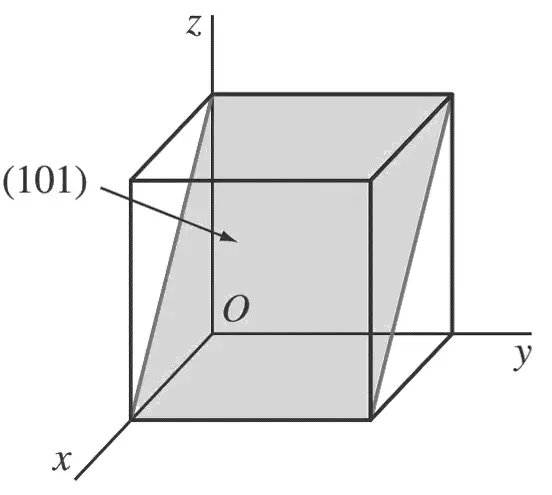
B. (1 1̄ 0)
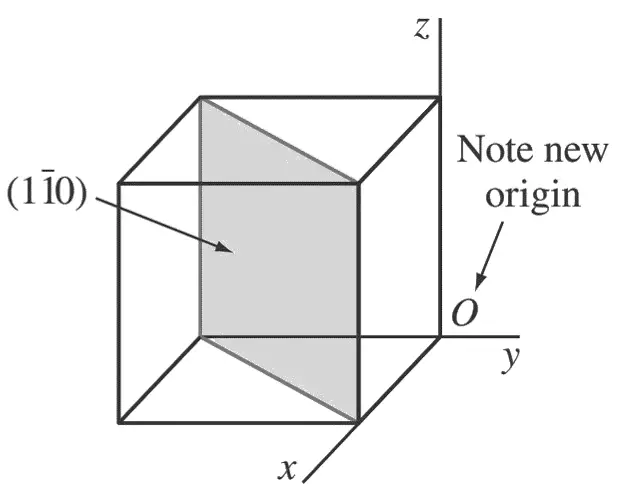
Primero determine los recíprocos de los índices de Miller del plano (1̄ 1 0). Estos son 1, −1, ∞.
El plano (1̄ 1 0) debe pasar por un cubo unitario en las intersecciones x = 1 e y = −1 y ser paralelo al eje z.
Tenga en cuenta que el origen de los ejes debe moverse a la parte inferior derecha del cubo.
C. (2 2 1)
Primero determine los recíprocos de los índices de Miller del plano (2 2 1). Estos son 1/2, 1/2, 1.
El plano (2 2 1) debe pasar por un cubo unitario en las intersecciones x = 1/ 2 , y = 1/ 2 y z = 1.
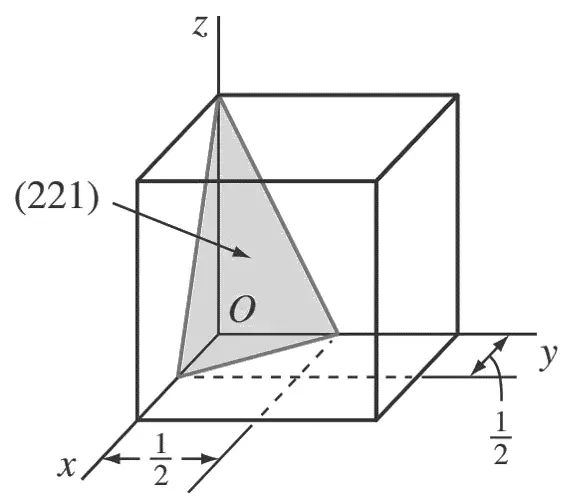
D
Las posiciones atómicas cuyos centros son intersecados por el plano (1 1 0) son (1, 0, 0), (0, 1, 0), (1,0, 1), (0, 1, 1) y ( 1 /2,1/2,1/2).
Estas posiciones están marcadas con círculos rellenos.
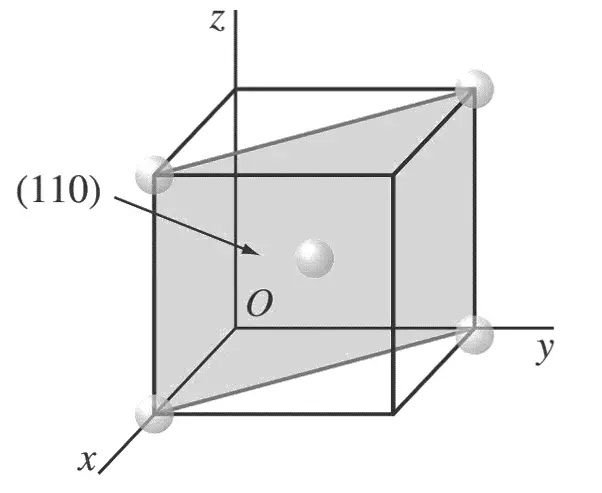
Una relación importante para el sistema cúbico, y sólo para el sistema cúbico, es que los índices direccionales de una dirección perpendicular a un plano cristalino son los mismos que los índices de Miller de ese plano.
Por ejemplo el [100] La dirección es perpendicular al plano cristalino (100). En estructuras cristalinas cúbicas, la distancia interplanar entre dos planos paralelos con los mismos índices de Miller se denota como dhkldonde h, k y l son los índices de Miller de los planos.
Esta distancia representa la distancia desde un origen seleccionado que contiene un plano y otro plano paralelo con los mismos índices más cercano a él. Por ejemplo, la distancia entre (110) los planos 1 y 2, es decir110en la siguiente figura es AB
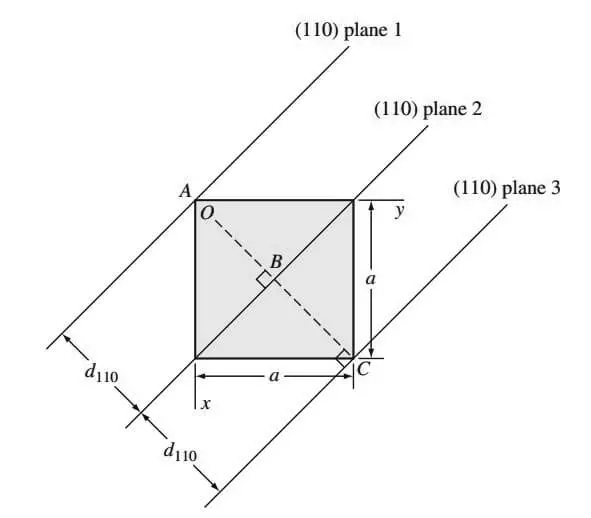
Además, la distancia entre (110) los planos 2 y 3 es d110 y corresponde a la longitud BC en la figura anterior.
De la geometría simple se puede demostrar que se trata de una estructura cristalina cúbica.
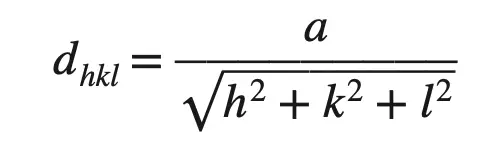
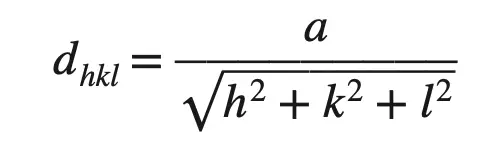
Dónde
Dhkl = distancia interplanar entre planos paralelos más cercanos con índices de Miller h, k y l
a = constante de red (arista del cubo unitario)
h, k, l = índices de Miller de los planos cúbicos considerados
Veamos un problema de ejemplo para determinar los índices de Miller del plano cristalográfico cúbico.
Problema de ejemplo sobre índices de Miller del plano cristalográfico cúbico
1. Determine los índices de Miller del plano cristalino cúbico que se muestra en la siguiente figura.
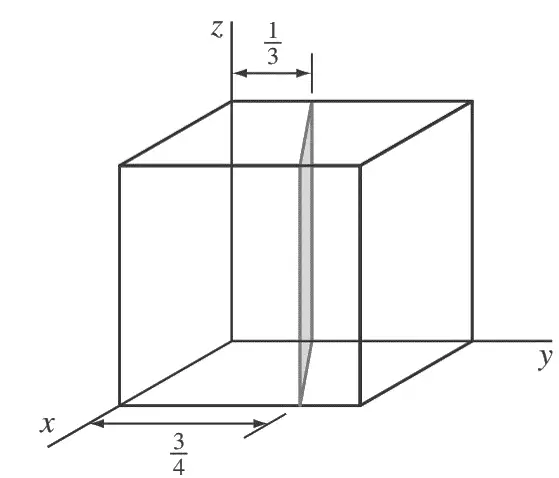
Respuesta:
Primero, transponga el plano paralelo al eje z 1/4 de unidad hacia la derecha a lo largo del eje y, como se muestra en la siguiente figura.
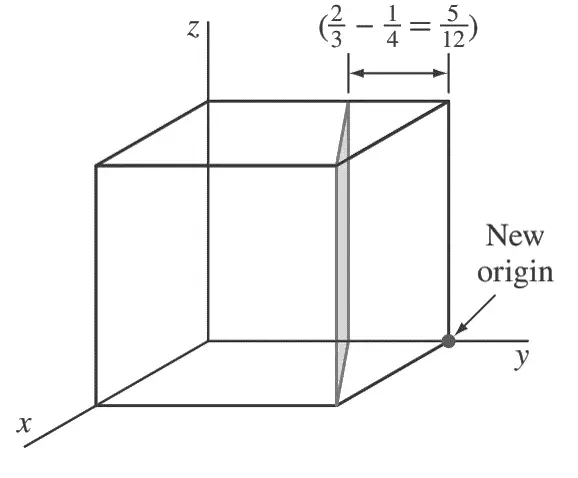
de modo que el plano interseca el eje x a una distancia unitaria del nuevo origen en la esquina inferior derecha posterior del cubo.
Los nuevos puntos de intersección del plano transpuesto con los ejes de coordenadas ahora son (+1, −5/ 12, ∞).
A continuación, tomamos los recíprocos de estas intersecciones para obtener (1, −12/5, 0).
Finalmente, eliminamos la fracción 12/5 para obtener (5 12̄ 0) para los índices de Miller de este nivel.
2. Determine los índices de Miller del plano cristalino cúbico que intersecta las coordenadas de posición (1, 1/4, 0), (1, 1,/12), (3/4, 1,/1 4) y todos los ejes de coordenadas.
Respuesta:
Solución
Primero, ubicamos las tres coordenadas de posición en A, B y C como se muestra en la siguiente figura.
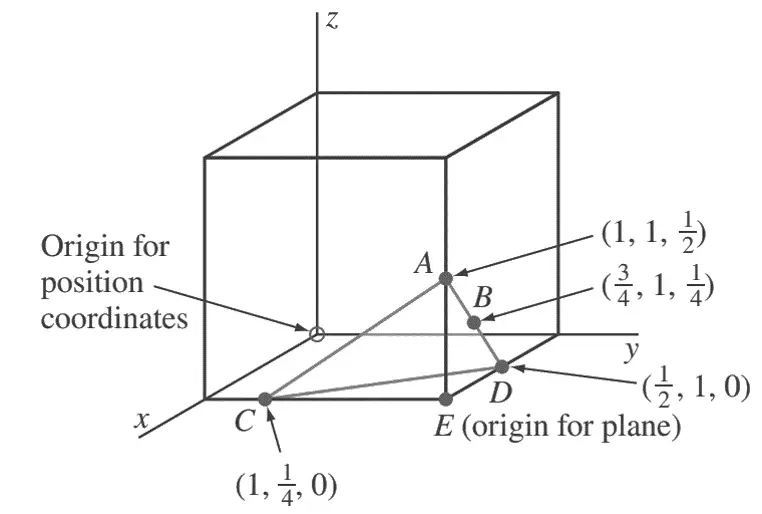
Luego conectamos A y B, extendemos AB a D y luego conectamos A y C.
Finalmente, conectamos A con C para completar la capa ACD.
El origen de este plano en el cubo se puede elegir en E, lo que da como resultado intersecciones del eje para el plano ACD en x = −1/2, y = −3/4 y z = 1/2.
Los recíprocos de estas intersecciones son −2, −4/3 y 2.
Al multiplicar estas intersecciones por 3 se elimina la fracción y se obtienen índices de Miller para el plano de (6̄ 4̄ 6).
3. El cobre tiene una estructura cristalina FCC y una celda unitaria con una constante de red de 0,361 nm.¿Cuál es su distancia interplanar d?220?
Respuesta:
Sabemos que la distancia interplanar entre planos paralelos más cercanos con índices de Miller h, k y l está dada por
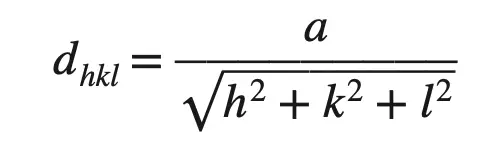
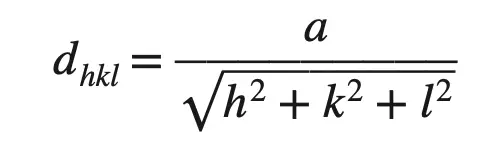
Dhkl = 0,361 nm/ √((2)2 + (2)2 + (0)2)
Dhkl = 0,128 nm
Índices del plano cristalino en celdas unitarias HCP
Los planos cristalinos en las celdas unitarias de HCP se identifican comúnmente mediante el uso de cuatro índices en lugar de tres. Los índices del plano cristalino de HCP, llamados índices de Miller-Bravais, se indican con las letras h, k, i y l y se indican entre paréntesis como (hkil).
Este índice hexagonal de cuatro dígitos se basa en un sistema de coordenadas de cuatro ejes, como se muestra en la siguiente figura en una celda unitaria HCP.
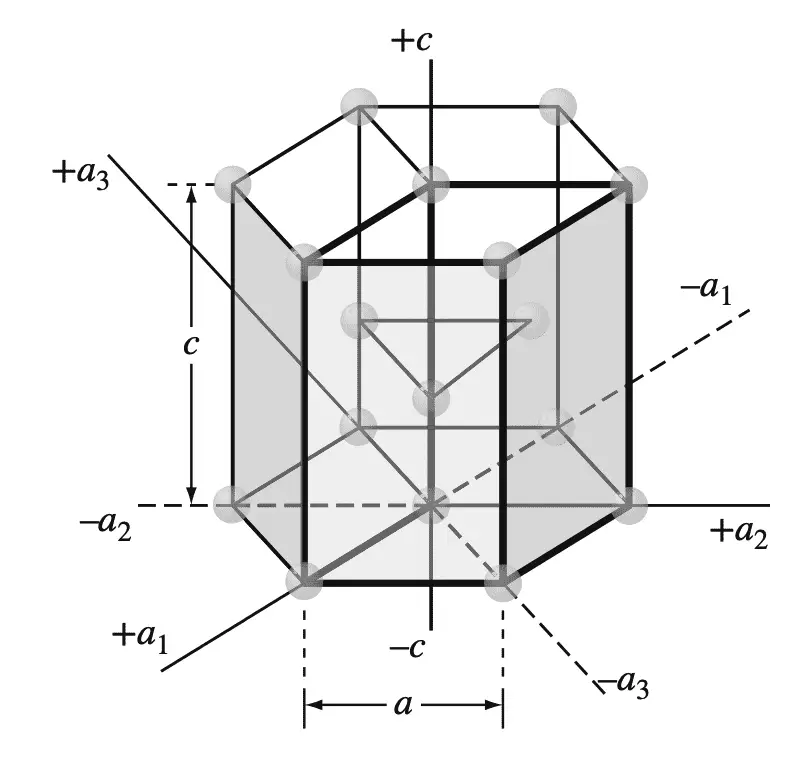
Los cuatro ejes de coordenadas (a1, a2, a3 y c) de la estructura cristalina de HCP.
Hay tres ejes basales, un1A2y un3, que forman un ángulo de 120° entre sí. El cuarto eje, o eje c, es el eje vertical ubicado en el centro de la celda unitaria.
La unidad de medida a lo largo de la a1A2y un3 Los ejes son la distancia entre los átomos a lo largo de estos ejes y se muestra en la figura anterior.
Cuando analicemos los niveles y direcciones del PS, usaremos tanto la “celda unitaria” como la “celda más grande” para representar conceptos. La unidad de medida a lo largo del eje c es la altura de la celda unitaria. Los recíprocos de las intersecciones que forman un plano cristalino con una1A2y un3 Los ejes dan los índices h, k e i, mientras que el recíproco de la intersección con el eje c da el índice l.
planos basales
Los planos basales de la celda unitaria HCP son planos muy importantes para esta celda unitaria y se muestran en la siguiente figura.
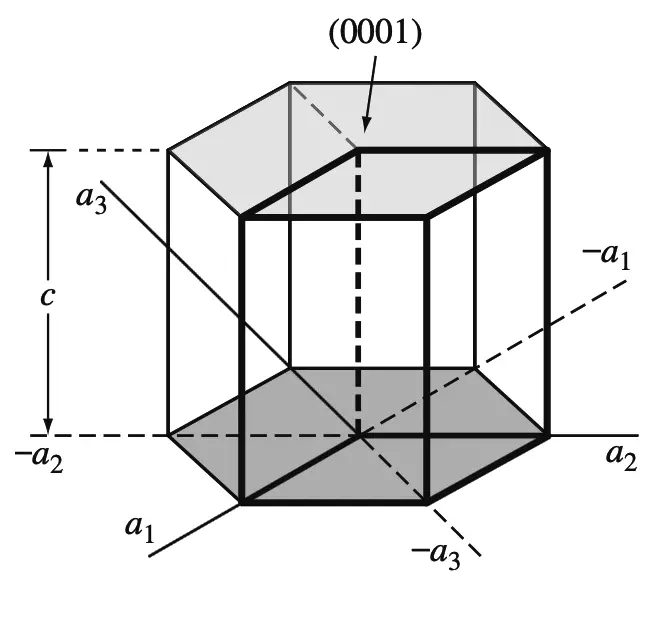
Dado que el plano base en la parte superior de la celda unitaria HCP en la figura anterior es paralelo a una1A2y un3 Ejes, los puntos de intersección de este plano con estos ejes se encuentran en el infinito.
Por lo tanto,
A1intercepción = ∞,
A2 interceptar = ∞,
A3intercepción = ∞.
Sin embargo, el eje c es uno porque el plano base superior intersecta el eje c a una distancia unitaria.
Cinterceptar = 1
Al formar los recíprocos de estas secciones se obtienen los índices de Miller-Bravais para el plano basal del HCP.
Así h = 0, k = 0, i = 0 y l = 1.
Por lo tanto, el nivel base de HCP es un nivel cero-cero-cero-uno o (0001).
niveles de prisma
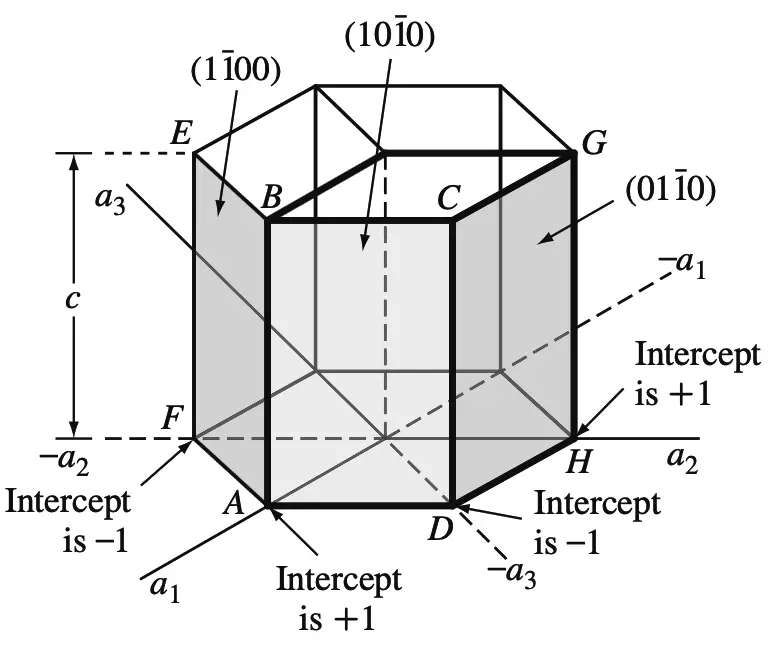
Índices de Miller-Bravais de planos cristalinos hexagonales: (a) planos base y (b) planos prismáticos
Usando el mismo método, los puntos de intersección del plano del prisma anterior (ABCD), como se muestra en la figura anterior, son un1intercepción = +1
A2 interceptar = ∞
A3intercepción = −1
Cinterceptar = ∞
Al formar los recíprocos de estas intersecciones se obtiene h = 1, k = 0, i = −1 y l = 0 o el plano (1 0 1̄ 0).
Asimismo, en la figura anterior, el plano del prisma ABEF tiene índices (1 1̄ 0 0) y el plano DCGH tiene índices (0 1 1̄ 0).
Todos los planos del prisma HCP se pueden identificar colectivamente como la familia de planos {1 0 1̄ 0}.
A veces, los niveles de HCP se identifican mediante solo tres índices (hkl), ya que h + k = −i.
Sin embargo, los índices (hkil) se utilizan más comúnmente porque revelan la simetría hexagonal de la celda unitaria HCP.
Índices direccionales en celdas unitarias HCP
Las direcciones en las celdas unitarias de HCP también suelen indicarse mediante cuatro índices u, v, t y w encerrados entre corchetes. [u v t w].
Los índices u, v y t son vectores reticulares en una1A2y un3 direcciones, y el índice w es un vector de cuadrícula en la dirección c.
Para mantener la coherencia de ambos índices HCP para niveles y direcciones, se acordó que u + v = −t para direcciones.
Determinemos ahora los índices hexagonales de Miller-Bravais para las direcciones a1A2y un3que son los ejes base positivos de la celda unitaria hexagonal.
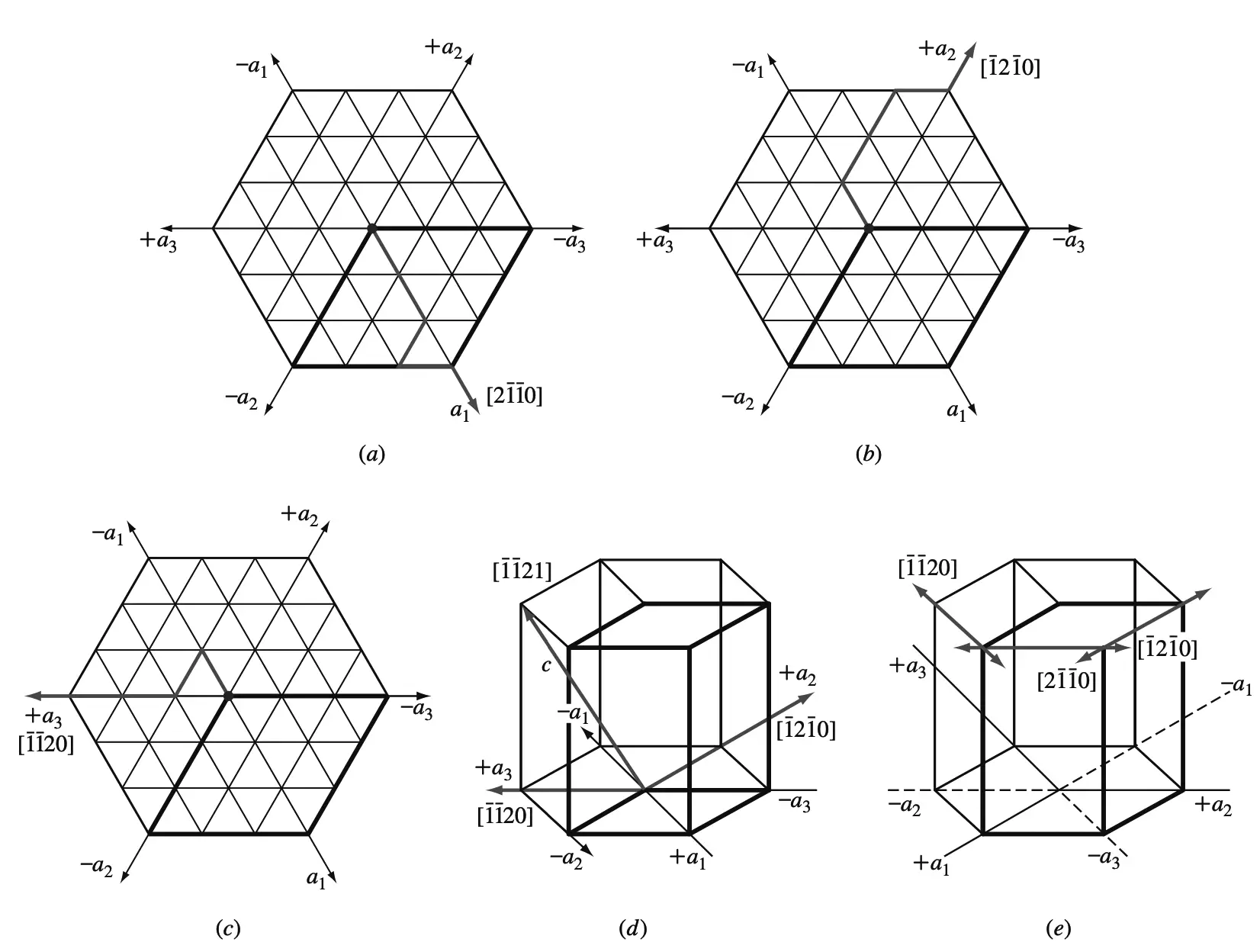
(A) +A1 Dirección del eje en el plano base,
(b) +a2 Dirección del eje en el plano base,
(c) +a3 Eje direccional en el plano base,
(D) +A3 Incluir eje direccional C Eje.
(e) Las direcciones de Miller-Bravais positivas y negativas se indican en la estructura cristalina hexagonal simple en el nivel basal superior.
La A1 Los índices direccionales se dan en la figura a, la a2 Índices direccionales en los paneles by a3 Índices direccionales en la figura c.
Si necesitamos especificar la dirección AC para un también3 Dirección, esto se muestra en la figura d.
La Figura e resume las direcciones positivas y negativas en el nivel basal superior de la estructura cristalina hexagonal simple.
[automatic_youtube_gallery type=»search» search=»¿Cómo calcular los índices de Miller para planos cristalográficos?
» limit=»1″]
Los índices de Miller para los planos cristalográficos
A veces es necesario referirse a planos de red específicos de átomos dentro de una estructura cristalina, o puede ser de interés conocer la orientación cristalográfica de un plano o grupo de planos en una red cristalina. Para identificar planos cristalográficos en estructuras cristalinas cúbicas o hexagonales, se utiliza el sistema de notación de Miller. Veamos cómo podemos calcular los índices de Miller para los planos cristalográficos en el sistema cúbico y en la estructura cristalina hexagonal.
Índices de Miller para los planos cristalográficos en el sistema cúbico
- Elige un plano que no pase por el origen en (0, 0, 0).
- Determina las intercepciones del plano en términos de los ejes cristalográficos x, y y z en un cubo unitario. Estas intercepciones pueden ser fraccionarias.
- Forma los recíprocos de estas intercepciones.
- Elimina las fracciones y determina el conjunto más pequeño de números enteros que estén en la misma proporción que las intercepciones. Estos números enteros son los índices de Miller del plano cristalográfico y se encluyen entre paréntesis sin el uso de comas. La notación (hkl) se utiliza para indicar los índices de Miller en un sentido general, donde h, k y l son los índices de Miller de un plano cristalino cúbico para los ejes x, y y z, respectivamente.
Por ejemplo, el plano (100) representa el plano uno-cero-cero, el plano (110) representa el plano uno-uno-cero y el plano (111) representa el plano uno-uno-uno.
Índices de Miller para los planos cristalográficos en la estructura cristalina hexagonal
- Elige un plano que no pase por el origen en (0, 0, 0).
- Determina las intercepciones del plano en términos de los ejes cristalográficos a1, a2, a3 y c de la celda unitaria hexagonal. Estas intercepciones pueden ser fraccionarias.
- Forma los recíprocos de estas intercepciones.
- Elimina las fracciones y determina el conjunto más pequeño de números enteros que estén en la misma proporción que las intercepciones. Estos números enteros son los índices de Miller-Bravais de los planos cristalográficos hexagonales y se encluyen entre paréntesis como (hki l).
Por ejemplo, el plano basal en la estructura cristalina hexagonal tiene los índices (0001), el plano prisma tiene los índices (1010) y el plano pirámide tiene los índices (1011).
Preguntas frecuentes sobre los índices de Miller para los planos cristalográficos
¿Cuál es la importancia de los índices de Miller en cristalografía?
Los índices de Miller son utilizados para identificar y describir planos cristalográficos en estructuras cristalinas cúbicas y hexagonales. Estos índices nos permiten entender la orientación de los planos en la red cristalina y determinar las distancias interplanares entre planos paralelos.
¿Cómo se calculan los índices de Miller para un plano cristalográfico?
Los índices de Miller se calculan tomando las intercepciones del plano con los ejes cristalográficos en una celda unitaria y formando los recíprocos de estas intercepciones. Luego, se eliminan las fracciones y se determina el conjunto más pequeño de números enteros que estén en la misma proporción que las intercepciones. Estos números enteros son los índices de Miller del plano.
¿Cuál es la relación entre los índices de Miller y las distancias interplanares?
En las estructuras cristalinas cúbicas, la distancia entre dos planos paralelos con los mismos índices de Miller se denomina distancia interplanar. Esta distancia se calcula utilizando la fórmula dhkl = a / √(h^2 + k^2 + l^2), donde a es la constante de red (longitud de la arista del cubo) y h, k y l son los índices de Miller del plano.
En las estructuras cristalinas hexagonales, la distancia interplanar se calcula de manera similar, pero utilizando los índices de Miller-Bravais y la fórmula dhkil = a / √(4h^2 + 4k^2 + i^2 + 3l^2), donde a es la constante de red.
Referencias:
