El esfuerzo de flexión es un concepto clave en la ingeniería estructural que determina la capacidad de un material para resistir fuerzas de flexión. En este artículo, exploraremos en profundidad qué es exactamente el esfuerzo de flexión y cómo se aplica en vigas curvas. Descubriremos los diferentes tipos de esfuerzo de flexión, las fórmulas utilizadas para calcularlo y cómo afecta a la resistencia y estabilidad de las estructuras curvas. Si quieres conocer más sobre este tema apasionante, ¡sigue leyendo!

Cuando un componente de una máquina se somete a una carga (carga estática o dinámica), sufre flexión a lo largo de su longitud debido a la tensión inducida en su interior. Esta tensión se llama tensión de flexión. Además, también se inducen otros tipos de estrés. Estos son esfuerzos de tracción, esfuerzos de compresión, esfuerzos cortantes, esfuerzos de apoyo y esfuerzos de torsión. En este caso, sólo debemos considerar la viga sometida a flexión pura para conocer el esfuerzo de flexión en vigas dobladas.

Esfuerzo de flexión

La tensión de flexión es la tensión normal creada en las vigas debido a la carga estática o dinámica aplicada. El estudio de la tensión de flexión en vigas difiere para vigas rectas y curvas. En este artículo, discutiremos la tensión de flexión en las vigas curvas.

Vigas curvas

En el artículo anterior hablamos de la tensión de flexión en vigas rectas (primera recta). Ahora discutiremos la tensión de flexión en vigas curvas (primera curva).

• Para una viga recta se supone que el eje del centro de masa y el eje neutro coinciden. Sin embargo, para vigas curvas se supone que el eje neutro y el eje del centro de gravedad no coinciden, sino que el eje neutro se desplaza hacia el centro de curvatura.
• Debido al desplazamiento del eje neutro hacia el centro de curvatura, la distribución de tensiones en la viga curva no es lineal.

¿Te has preguntado dónde utilizamos las vigas curvas?

¿Has visto el gancho de la grúa?

Sí, ganchos de grúa y eslabones de cadena, perforadoras, prensas y cepilladoras. Estos son los mejores ejemplos de vigas inicialmente dobladas.

Esfuerzo de flexión en vigas curvas.

Considere una viga inicialmente curvada sometida al momento flector. METRO. Se aplican los mismos supuestos que para las barras rectas (mencionadas al final del artículo). Las siguientes son las cosas notables que observaremos cuando encontremos la tensión de flexión en las vigas dobladas.

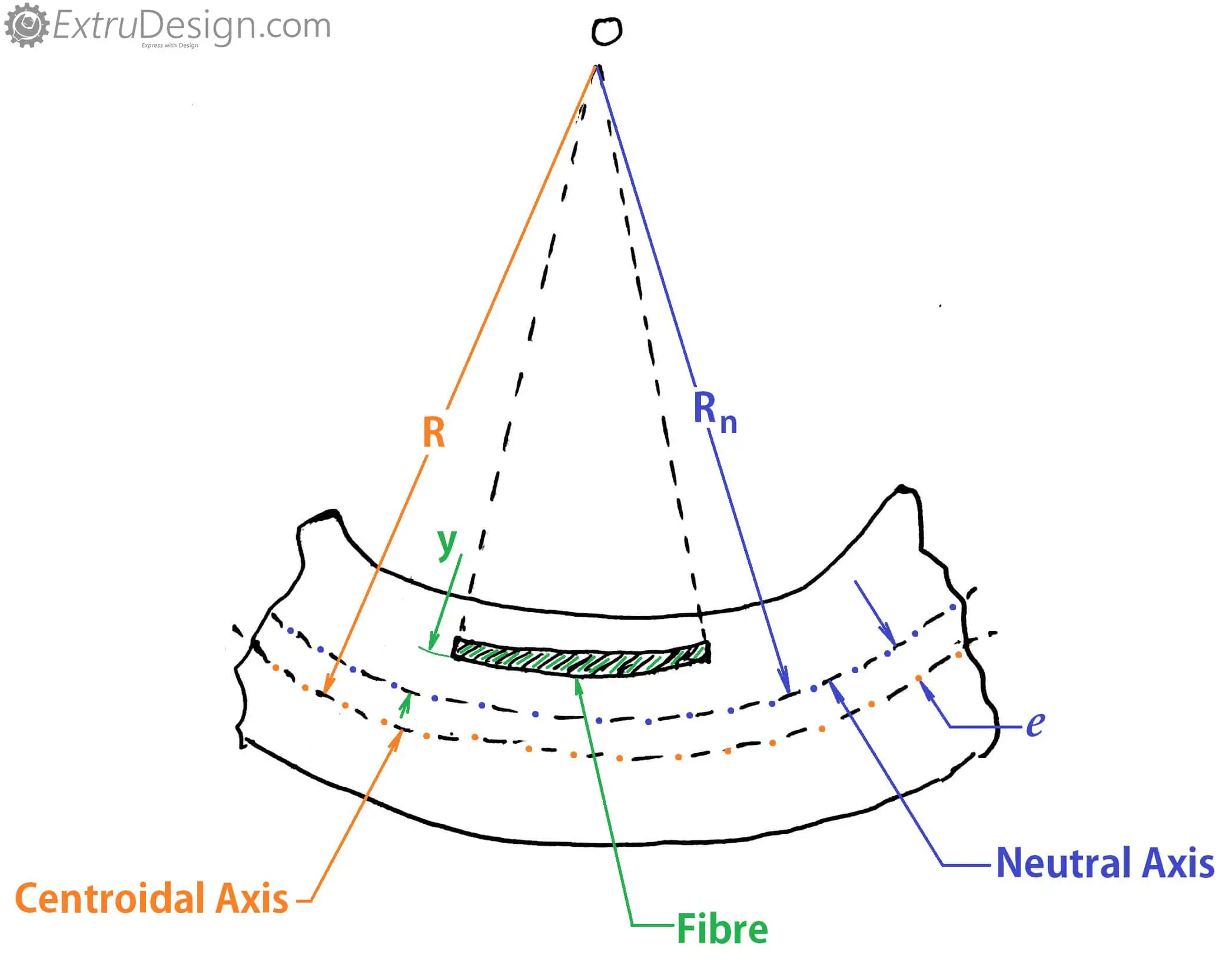
1. En vigas curvas, la tensión de flexión inducida en las fibras internas tiende a ser de tracción, mientras que las fibras externas tienden a comprimirse.
2. Si la sección es simétrica (secciones de vigas en I circulares o rectangulares), el esfuerzo máximo de flexión se induce en la fibra interior.
3. Si la sección transversal es asimétrica, la tensión de flexión máxima se puede observar en las fibras internas o externas. (Ver conclusión)

La tensión de flexión sobre cada fibra a una distancia y del eje neutro está dada por

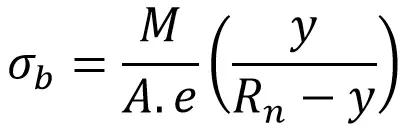
Dónde

M = momento flector que actúa en la sección dada alrededor del eje del centro de gravedad.

A = área de la sección transversal

mi = Distancia del eje del centro de gravedad al eje neutro R – R_norte

R = radio de curvatura del eje del centro de gravedad

R_norte = Radio de curvatura del eje neutro

y = distancia entre el eje neutro y la fibra considerada cuyo esfuerzo de flexión se tuvo que calcular

(+ve para la distancia al centro de curvatura, -ve para la distancia desde el centro de curvatura)

De la ecuación anterior podemos encontrar la tensión de flexión de la viga curva en cada fibra.

Consideraciones sobre la tensión de flexión en vigas curvas

Se deben hacer algunas consideraciones al determinar el esfuerzo de flexión de las vigas dobladas. Son los siguientes

• Hay que tener en cuenta que el material sea el mismo en toda la viga (material homogéneo).
• Debe obedecer la ley de Hooke (la tensión es directamente proporcional a la deformación en la viga).
• Cada capa de la viga debe expandirse o contraerse libre e independientemente.
• La carga debe aplicarse en el plano de flexión (plano de curvatura).
• El módulo de elasticidad debe ser el mismo tanto para tensión como para compresión.

Diploma

a) Como se mencionó anteriormente: Si la sección es asimétrica, el esfuerzo de flexión máximo se induciría ya sea en el interior de la fibra o en el exterior de la fibra. Usando estas fórmulas podemos calcular la tensión de flexión.

El esfuerzo de flexión máximo en el interior de la fibra está dado por

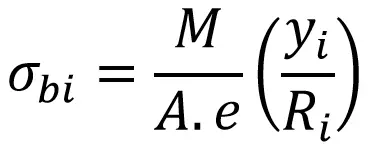
Dónde

j_I = Distancia entre eje neutro y fibra interior = R_norte-R_I

R_I = Radio de curvatura de la fibra interior

El esfuerzo de flexión máximo en el exterior de la fibra está dado por

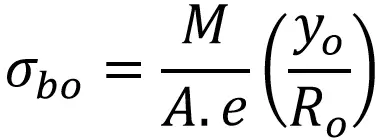
Y_oh = Distancia entre eje neutro y fibra exterior = R_oh -R_norte

R_oh = Radio de curvatura de la fibra exterior

b) Además del momento flector, para carga axial, la carga axial se puede sumar alfabéticamente al esfuerzo de flexión para obtener el esfuerzo resultante en la viga curva dada.

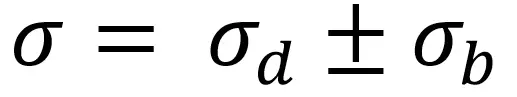
[automatic_youtube_gallery type=»search» search=» ¿Qué es el esfuerzo de flexión? ¿Esfuerzo de flexión en vigas curvas?

» limit=»1″]

La tensión de flexión en vigas curvas

Cuando un componente de una máquina se somete a una carga (estática o dinámica), experimentará flexión a lo largo de su longitud debido al estrés inducido en él. Este estrés se conoce como tensión de flexión. Además, también se inducen otros tipos de estrés, como la tensión de tracción, la tensión de compresión, la tensión de corte, la tensión de apoyo y la tensión torsional. En este caso, suponemos que la viga solo está sometida a flexión pura para encontrar la tensión de flexión en vigas curvas.

Tensión de Flexión

La tensión de flexión es el estrés normal inducido en las vigas debido a una carga estática o dinámica aplicada. El estudio de la tensión de flexión en las vigas será diferente para las vigas rectas y las vigas curvas. En este artículo, discutiremos la tensión de flexión en las vigas curvas.

Vigas Curvas

En el artículo anterior, discutimos la tensión de flexión en vigas rectas (inicialmente rectas). Ahora vamos a discutir la tensión de flexión en vigas curvas (inicialmente curvas).

En una viga recta, se considera que el eje centroidal y el eje neutro coinciden. Pero en vigas curvas, se considera que el eje neutro y el eje centroidal no coinciden, sino que el eje neutro se desplazará hacia el centro de curvatura. Debido al desplazamiento del eje neutro hacia el centro de curvatura, la distribución de esfuerzos en la viga curva será no lineal.

¿Alguna vez has visto el gancho de una grúa? ¿O los eslabones de una cadena, punzones, prensas y cepillos? Estos son los mejores ejemplos de vigas inicialmente curvas.

Tensión de Flexión en Vigas Curvas

Consideremos una viga inicialmente curva que está sometida a un momento de flexión M. Se hacen las mismas suposiciones que en las vigas rectas (mencionadas al final del artículo). Las siguientes son las cosas destacables que se observarán al encontrar la tensión de flexión en las vigas curvas.

• En las vigas curvas, la tensión de flexión inducida en las fibras internas tiende a ser de tracción, mientras que las fibras externas tienden a ser de compresión.
• Si la sección es simétrica (secciones circulares o de viga de tipo I), la máxima tensión de flexión se inducirá en las fibras internas.
• Si la sección es asimétrica, entonces la máxima tensión de flexión puede observarse en las fibras internas o externas (ver conclusión).

La tensión de flexión en cualquier fibra a una distancia y del eje neutro se calcula mediante la siguiente fórmula:

Sigma = (M * e) / (A * y)

Donde:

M = Momento de flexión que actúa en la sección dada con respecto al eje centroidal.

A = Área de la sección transversal.

e = Distancia desde el eje centroidal al eje neutro R – Rn

R = Radio de curvatura del eje centroidal.

Rn = Radio de curvatura del eje neutro.

y = Distancia entre el eje neutro y la fibra considerada para la cual se necesita calcular la tensión de flexión.

(+ para la distancia hacia el centro de curvatura, – para la distancia lejos del centro de curvatura)

A partir de la ecuación anterior, podemos calcular la tensión de flexión para la viga curva en cualquier fibra.

Consideraciones en la Tensión de Flexión en Vigas Curvas

Existen algunas consideraciones que se deben tener en cuenta al encontrar la tensión de flexión en las vigas curvas. Son las siguientes:

• Se debe considerar que el material a lo largo de la viga es el mismo (material homogéneo).
• Debe cumplir con la ley de Hooke (el estrés es directamente proporcional a la deformación en la viga).
• Cada capa de la viga debe expandirse o contraerse libre e independientemente.
• La carga debe aplicarse en el plano (plano de curvatura) de flexión.
• El módulo de elasticidad debe ser el mismo tanto para la tensión como para la compresión.

Conclusión

a) Como mencionamos anteriormente, si la sección es asimétrica, entonces la máxima tensión de flexión se inducirá en las fibras internas o externas. Mediante el uso de estas fórmulas, podemos calcular la tensión de flexión.

La máxima tensión de flexión en las fibras internas se calcula utilizando la siguiente fórmula:

Sigma_i = (M * yi) / (A * Rn)

Donde:

yi = Distancia entre el eje neutro y la fibra interna = Rn – Ri

Ri = Radio de curvatura de la fibra interna

La máxima tensión de flexión en las fibras externas se calcula utilizando la siguiente fórmula:

Sigma_o = (M * Yo) / (A * Rn).

Donde:

Yo = Distancia entre el eje neutro y la fibra externa = Ro – Rn

Ro = Radio de curvatura de la fibra externa

b) Además del momento de flexión, si hay una carga axial, ésta puede sumarse algebraicamente a la tensión de flexión para obtener el esfuerzo resultante en la viga curva.