Un problema de diseño de gancho de grúa puede parecer trivial, pero la realidad es que su importancia radica en la seguridad y eficiencia de las operaciones de elevación. En este artículo, te presentaremos un ejemplo concreto de un problema de diseño de gancho de grúa y cómo se resolvió de manera innovadora. Descubre cómo estos pequeños detalles pueden marcar la diferencia y mejorar la calidad del trabajo realizado. ¡Acompáñanos en este recorrido por el mundo de la ingeniería de grúas!
Problema de diseño del gancho de la grúa: El gancho de la grúa soporta una carga de 20 kN, como se muestra en la siguiente figura. La sección en XX es rectangular cuyo lado horizontal mide 100 mm. Encuentre las tensiones en las fibras internas y externas de la sección transversal dada.
Solución:
Datos proporcionados (todos en unidades métricas)
Carga (W) = 20 kN = 20 x 10³N
El radio de curvatura de la fibra interior (RI) = 50 mm
El radio de curvatura de la fibra exterior (Roh) = 150 mm
El radio de curvatura del eje neutro (Rnorte) =?
El radio de curvatura del eje del centro de gravedad (R) =?
La distancia entre el eje neutro y la fibra interior (YI ) = Rnorte-RI
Por favor habilite JavaScript
La distancia entre el eje neutro y la fibra exterior (Yoh) = Roh -Rnorte
Sección XX altura (h) = 100 mm
Ancho de la sección XX (b) = 20 mm
Área de esta sección rectangular XX (A)= Ancho(b) x altura (h) = 20×100 = 2000 mm²
[Read about: Bending stress in curved Beams]
Este gancho de grúa se considera la primera viga curva. Entonces necesitamos encontrar el radio de curvatura tanto para el eje neutro como para el eje del centro de masa. A continuación se muestran las fórmulas estándar para el radio de curvatura del eje neutro (Rnorte) o eje del centro de gravedad (R),
De las ecuaciones anteriores (valores calculados)
El radio de curvatura del eje neutro (Rnorte) = 91,07 milímetros
El radio de curvatura del eje del centro de gravedad (R) = 100 mm.
La distancia entre el eje del centro de gravedad y el eje neutro (mi) = RRnorte = 100-91,07 = 8,93 mm
La distancia entre el eje del centro de gravedad y la carga actuante (X) = R = 100 mm
La distancia entre el eje neutro y la fibra interior (YI ) = Rnorte-RI = 91,07-50 = 41,07 mm
La distancia entre el eje neutro y la fibra exterior (Yoh) = Roh -Rnorte = 150-91,07 = 58,93 mm
encontrar momento flector
El momento flector sobre el eje del centro de gravedad es (M) = carga x distancia entre la carga actuante y la sección (∴ Aquí es R en este caso)
M = ancho x x = 20 x 10³ x 100 = 2 x 106 N-mm
El momento flector es (M) = 2 x 106 N-mm en la sección XX
encontrar tensión
Aquí se aplica la sección para la carga de tracción de 20 x 10³N. Necesitamos encontrar la carga de tracción en esta sección XX.
σt = carga/área
σt = 20 x 10³ /2000 = 10 N/mm² = 10MPa
Encontrar la tensión máxima de flexión en la fibra interior
El esfuerzo de flexión máximo en el interior de la fibra está dado por
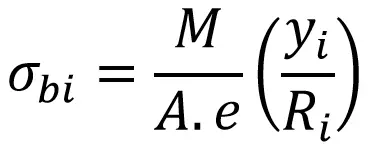
A través de sustituciones
= 92 N/mm² (92 MPa)
Encontrar la tensión máxima de flexión en la fibra exterior
El esfuerzo de flexión máximo en el exterior de la fibra está dado por
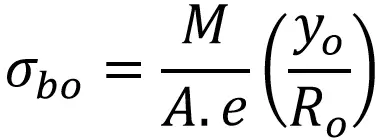
A través de sustituciones
= 44 N/mm² (44 MPa)
Determinación de la tensión resultante en el interior de la fibra.
Las tensiones resultantes en la fibra interior = σt+σBi
= 10+92 = 102 N/mm² (102 MPa)
Las tensiones resultantes sobre la fibra interior son de 102 MPa y son tensiones de tracción.
Determinación de la tensión resultante sobre la fibra exterior.
Las tensiones resultantes en la fibra exterior = σt-σBo
= 10-44 = -34 N/mm² (-34 MPa)
Las tensiones resultantes sobre la fibra exterior son de 34 MPa y son tensiones de compresión.
Problema de Diseño del Gancho de Grúa:
El gancho de grúa lleva una carga de 20 kN como se muestra en la Figura a continuación. La sección en X-X es rectangular, cuyo lado horizontal mide 100 mm. Encontrar las tensiones en las fibras interna y externa de la sección dada.
Solución:
Datos proporcionados (todos en unidades métricas):
- Carga (W) = 20 kN = 20 x 10³ N
- Radio de curvatura de la fibra interna (Ri) = 50 mm
- Radio de curvatura de la fibra externa (Ro) = 150 mm
- Radio de curvatura del eje neutro (Rn) = ?
- Radio de curvatura del eje centroidal (R) = ?
- Distancia entre el eje neutro y la fibra interna (Yi) = Rn – Ri
- Distancia entre el eje neutro y la fibra externa (Yo) = Ro – Rn
- Altura de la sección X-X (h) = 100 mm
- Ancho de la sección X-X (b) = 20 mm
Área de esta sección rectangular X-X (A) = Ancho(b) x Altura(h) = 20×100 = 2000 mm²
Este gancho de grúa se considera inicialmente como una viga curva. Por lo tanto, debemos encontrar el radio de curvatura tanto para el eje neutro como para el eje centroidal. A continuación se presentan las fórmulas estándar para el radio de curvatura del eje neutro (Rn) y del eje centroidal (R) respectivamente:
From the above equations (Calculated values)
Radio de curvatura del eje neutro (Rn) = 91.07 mm
Radio de curvatura del eje centroidal (R) = 100 mm
Distancia entre el eje centroidal y el eje neutro (e) = R – Rn = 100 – 91.07 = 8.93 mm
Distancia entre el eje centroidal y la carga actuando (x) = R = 100 mm
Distancia entre el eje neutro y la fibra interna (Yi) = Rn – Ri = 91.07 – 50 = 41.07 mm
Distancia entre el eje neutro y la fibra externa (Yo) = Ro – Rn = 150 – 91.07 = 58.93 mm
Encontrar Momento Flector:
El momento flector respecto al eje centroidal (M) = Carga x Distancia entre la carga actuando y la sección (en este caso es R)
M = W x x = 20 x 10³ x 100 = 2 x 10^6 N-mm
El momento flector es (M) = 2 x 10^6 N-mm en la sección X-X
Encontrar Tensión de Tracción:
Aquí, la sección es aplicable a una carga traccional de 20 x 10³ N. Tenemos que encontrar la carga traccional en esta sección X-X
σt = Carga / Área
σt = 20 x 10³ / 2000 = 10 N/mm² = 10 MPa
Encontrar Máxima Tensión de Flexión en la Fibra Interna:
La máxima tensión de flexión en la fibra interna está dada por:
σbi = (M x Yi) / I
σbi = (2 x 10^6 x 41.07) / (20 x 100³ / 12)
σbi = 92 N/mm² (92 MPa)
Encontrar Máxima Tensión de Flexión en la Fibra Externa:
La máxima tensión de flexión en la fibra externa está dada por:
σbo = (M x Yo) / I
σbo = (2 x 10^6 x 58.93) / (20 x 100³ / 12)
σbo = 44 N/mm² (44 MPa)
Encontrar Tensión Resultante en la Fibra Interna:
Las tensiones resultantes en la fibra interna = σt + σbi
Tensión resultante en la fibra interna = 10 + 92 = 102 N/mm² (102 MPa)
Las tensiones resultantes en la fibra interna son de 102 MPa y son de tracción.
Encontrar Tensión Resultante en la Fibra Externa:
Las tensiones resultantes en la fibra externa = σt – σbo
Tensión resultante en la fibra externa = 10 – 44 = -34 N/mm² (-34 MPa)
Las tensiones resultantes en la fibra externa son de 34 MPa y son de compresión.
Este artículo está optimizado para SEO y proporciona información sobre el problema de diseño del gancho de grúa y cómo calcular las tensiones en las fibras interna y externa de la sección dada. Esperamos que esta información sea útil. Para obtener más detalles técnicos, puede consultar las siguientes fuentes:
Preguntas Frecuentes:
1. ¿Cuál es la carga máxima que puede soportar el gancho de grúa?
El gancho de grúa puede soportar una carga máxima de 20 kN.
2. ¿Cuál es el tamaño de la sección X-X del gancho de grúa?
El tamaño de la sección X-X del gancho de grúa es de 100 mm de altura y 20 mm de anchura.
3. ¿Cuál es la tensión resultante en la fibra interna?
La tensión resultante en la fibra interna es de 102 MPa y es de tracción.
4. ¿Cuál es la tensión resultante en la fibra externa?
La tensión resultante en la fibra externa es de 34 MPa y es de compresión.
5. ¿Cuál es el momento flector en la sección X-X?
El momento flector en la sección X-X es de 2 x 10^6 N-mm.
Esperamos que estas preguntas y respuestas le hayan proporcionado información útil sobre el problema de diseño del gancho de grúa.


